
题目列表(包括答案和解析)
7.已知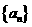 是等差数列,
是等差数列,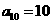 ,其前10项和
,其前10项和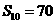 ,则其公差
,则其公差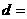 ( )
( )
A.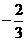 B.
B.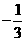 C.
C.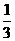 D.
D.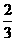
6.利用斜二测画法得到:三角形的直观图是三角形;‚平行四边形的直观图是平行四边形;ƒ正方形的直观图是正方形;④菱形的直观图是菱形。以上结论正确的是( )
A. ①② B.① C. ③④ D.①②③④
5.在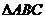 中,已知
中,已知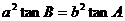 ,则该
,则该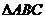 的形状为( )
的形状为( )
A. 等腰三角形 B. 直角三角形 C.正三角形 D.等腰或直角三角形
4.下列关于棱柱的描述中,正确的是( )
A.底面是正方形的四棱柱是正方体 B.棱柱只有两个面互相平行
C.棱柱所有的面都是平行四边形 D.底面为六边形的棱柱是六棱柱
3.不等式组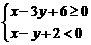 表示的平面区域是( )
表示的平面区域是( )

A. B. C. D.
2.在等比数列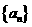 中,
中,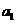 和
和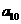 是方程
是方程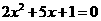 的两个根,则
的两个根,则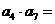 ( )
( )
A.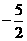 B.
B.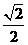 C.
C.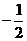 D.
D.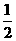
1.若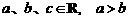 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A. 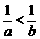 B.
B. 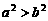 C.
C. 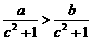 D.
D. 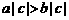
22、(本小题满分12分)
设有关于x的一元二次方程x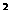 -2ax+b
-2ax+b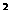 =0.
=0.
(1)若a是从0、1、2、3四个数中任取的一个数,b是从0、1、2三个数中任取的一个数,求上述方程没有实根的概率。
(2))若a是从区间[0,3]内任取的一个数,b=2,求上述方程没有实根的概率。
解:设事件A为“方程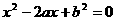 无实根”
无实根”
当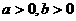 时,方程
时,方程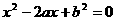 无实根的充要条件为
无实根的充要条件为
Δ=4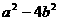 =4(
=4(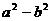 )< 0, 即
)< 0, 即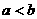
(1)基本事件共12个:(0,0)(0,1),(0,2),(1,0)(1,1),(1,2),(2,0),(2,1),
(2,2),(3,0),(3,1),(3,2)。其中第一个数表示a的取值,第二个数表示b的取值。 3分
事件A包含3个基本事件(0,1),(0,2)(1,2), 5分
事件A发生的概率为P(A)=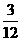 =
=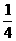 。
6分
。
6分
(2)试验的所有基本事件所构成的区域为: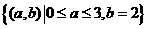 , 8分
, 8分
其中构成事件B的区域为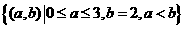 10分
10分
所以所求概率为P(B)=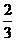 。
12分
。
12分
|

|
版权所有:()
版权所有:()
21、(本小题满分12分)
设函数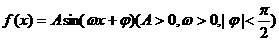 的最高点D的坐标为(
的最高点D的坐标为(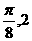 ),由最高点D运动到相邻最低点时,函数图形与
),由最高点D运动到相邻最低点时,函数图形与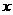 的交点的坐标为(
的交点的坐标为(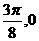 );
);
(1)求函数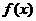 的解析式.
的解析式.
(2)当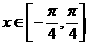 时,求函数
时,求函数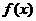 的最大值和最小值以及分别取得最大值和最小值时相应的自变量
的最大值和最小值以及分别取得最大值和最小值时相应的自变量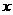 的值.
的值.
(3)将函数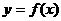 的图象向右平移
的图象向右平移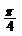 个单位,得到函数
个单位,得到函数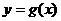 的图象,求函数
的图象,求函数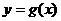 的单调减区间.
的单调减区间.
.解:(1)∵由最高点D(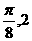 )运动到相邻最低点时,函数图形与
)运动到相邻最低点时,函数图形与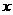 的交点的坐标为(
的交点的坐标为(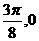 ), ∴
), ∴ ,
…………………2分
,
…………………2分
从而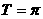 ,
,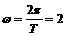 ,
,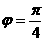 ………………3分
………………3分
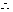 函数解析式为
函数解析式为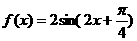 ………………4分
………………4分
(2)由(1)得函数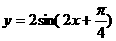 ,
,
当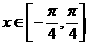 时,
时,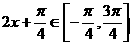 .
………………5分
.
………………5分
∴当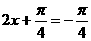 ,即
,即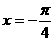 时,函数
时,函数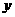 取得最小值
取得最小值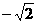 . ………………7分
. ………………7分
当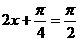 ,即
,即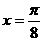 时,函数
时,函数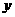 取得最大值2.
………………9分
取得最大值2.
………………9分
(3)由题意得,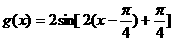 ,
,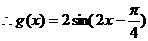 ,…………10分
,…………10分
由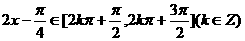 得,
得,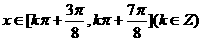
…………………11分
即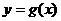 的单调减区间为
的单调减区间为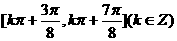 . …………………12分
. …………………12分
20、已知角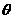 的终边上有一点P(
的终边上有一点P(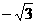 ,m),且
,m),且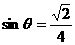 m,试求
m,试求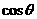 与
与 的值。
的值。
解:当m=0时,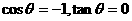 ;
4分
;
4分
当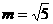 时,
时,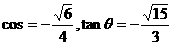 ,
8分
,
8分
当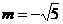 时,
时, 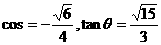 12分
12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com