
题目列表(包括答案和解析)
3.若tanα=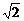 ,则
,则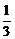 sin2α+cos2α的值是 ( )
sin2α+cos2α的值是 ( )
A.-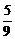 B.
B.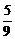 C.5 D.-5
C.5 D.-5
2.定义在R上的偶函数f(x)满足f(x)=f(x+2),当x∈[3,4]时,f(x)= x-2,则 ( )
A.f(sin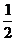 )<f(cos
)<f(cos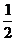 ) B.f(sin
) B.f(sin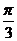 )>f(cos
)>f(cos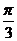 )C.f(sin1)<f(cos1) D.f(sin
)C.f(sin1)<f(cos1) D.f(sin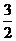 )>f(cos
)>f(cos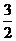 )
)
1.与-463°终边相同的角可以表示为(k∈Z) ( )
A.k·360°+463°B.k·360°+103°C.k·360°+257°D.k·360°-257°
22. (Ⅲ)从样本中身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm之间的概率。
解 (Ⅰ)样本中男生人数为40 ,由分层出样比例为10%估计全校男生人数为400。
(Ⅱ)有统计图知,样本中身高在170~185cm之间的学生有14+13+4+3+1=35人,样本容量为70 ,所以样本中学生身高在170~185cm之间的频率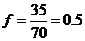 故有f估计该校学生身高在170~180cm之间的概率
故有f估计该校学生身高在170~180cm之间的概率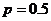
(Ⅲ)样本中身高在180~185cm之间的男生有4人,设其编号为①,②,③,④
样本中身高在185~190cm之间的男生有2人,设其编号为⑤,⑥
从上述6人中任取2人的树状图为:

故从样本中身高在180~190cm之间的男生中任选2人得所有可能结果数为15,求至少有1人身高在185~190cm之间的可能结果数为9,因此,所求概率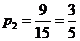
20.解:(Ⅰ)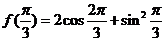 =
=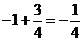
(Ⅱ)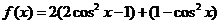
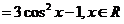 因为
因为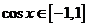 ,所以,当
,所以,当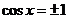 时
时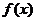 取最大值2;当
取最大值2;当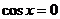 时,
时,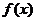 取最小值-1。
取最小值-1。
|

19.解:由题意,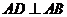 ,所以
,所以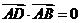 ,
,
又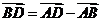 ,
,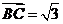
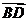 ,所以
,所以
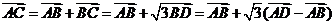
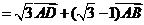 ,
,
所以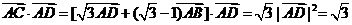 .
.
18.解析:(I)从袋子中随机取两个球,其一切可能的结果组成的基本事件有1和2,1和3,1和4,2和3,2和4,3和4,共6个。
从袋中随机取出的球的编号之和不大于4的事件共有1和2,1和3两个。
因此所求事件的概率为1/3。
(II)先从袋中随机取一个球,记下编号为m,放回后,在从袋中随机取一个球,记下编号为n,其一切可能的结果(m, n)有:
(1,1)(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1)(3,2), (3,3) (3,4),(4,1) (4,2),(4,3)(4,4),共16个
有满足条件n≥ m+2 的事件为(1,3) (1,4) (2,4),共3个
所以满足条件n ≥ m+2 的事件的概率为 P=3/16
故满足条件n<m+2 的事件的概率为 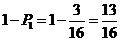
17. 解析:原式=lg(sinx+cosx)+lg(cosx+sinx)-lg(sinx+cosx)2=0.
16. 解析:考查互斥事件概率公式 P(A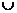 B)=
B)=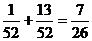
15. 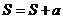
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com