
题目列表(包括答案和解析)
1.重点:展示点到直线的距离公式的探求思维过程.
(三)知识渗透点
由特殊到一般、由感性认识上升到理性认识是人们认识世界的基本规律.
(二)能力训练点
培养学生数形结合能力,综合应用知识解决问题的能力、类比思维能力,训练学生由特殊到一般的思想方法.
(一)知识教学点
点到直线距离公式的推导思想方法及公式的简单应用.
3.x2+y2-x+7y-32=0
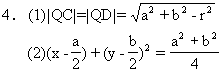
2.证明两圆连心线的长等于两圆半径之和
4.由圆外一点Q(a,b)向圆x2+y2=r2作割线交圆于A、 B两点,向圆x2+y2=r2作切线QC、QD,求:
(1)切线长;
(2)AB中点P的轨迹方程.
作业答案:
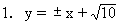
3.求经过两圆x2+y2+6x-4=0和x2+y2+6y-28=0的交点,并且圆心在直线x-y-4=0上的圆的方程.
2.求证:两圆x2+y2-4x-6y+9=0和x2+y2+12x+6y-19=0相外切.
(三)巩固练习
1.已知圆的方程是x2+y2=1,求:
(1)斜率为1的切线方程;

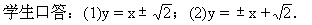
2.(1)圆(x-1)2+(y+2)2=4上的点到直线2x-y+1=0的最短距离是
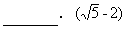
(2)两圆C1∶x2+y2-4x+2y+4=0与C2∶x2+y2+2x-6y-26=0的位置关系是______.(内切)
由学生口答.
3.未经过原点,且过圆x2+y2+8x-6y+21=0和直线x-y+5=0的两个交点的圆的方程.
分析:若要先求出直线和圆的交点,根据圆的一般方程,由三点可求得圆的方程;若没过交点的圆系方程,由此圆系过原点可确定参数λ,从而求得圆的方程.由两个同学演板给出两种解法:
解法一:
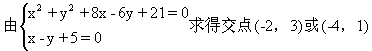
设所求圆的方程为x2+y2+Dx+Ey+F=0.
∵(0,0),(-2,3),(-4,1)三点在圆上,
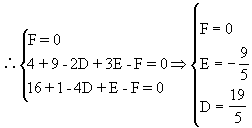
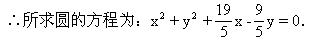
解法二:
设过交点的圆系方程为:
x2+y2+8x-6y+21+λ(x-y+5)=0.
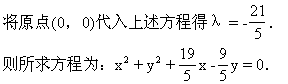
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com