5．　 下列命题中，真命题的个数为……(　 )

(1)　　　 垂直于同一平面的两直线平行

(2)　　　 与同一平面成等角的两直线平行

(3)　　　 四面体的四个表面最多可以有4个直角三角形

(4)　　　 和一对异面直线都垂直的直线有且只有一条

(5)　　　 侧面都是矩形的棱柱是长方体

A、1　　　　　　　　 B、2　　　　　　　　 C、3　　　　　　　　 D、4

4．　 长方体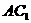中，AB=15，BC=8，则与平面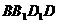的距离为……(　 )

A、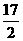　　 B、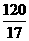　　 C、8　　 D、15

3．　 若一个角的两边和另一个角的两边分别平行，则这两个角……(　 )

A、相等　 B、互余　 C、互补　 D、相等或互补

2．　 若a和b是异面直线，b和c是异面直线，则……(　 )

A、a和c平行　 B、a和c相交

　 C、a和c是异面直线　 D、a和c或平行或相交或异面

1．　 两个不重合的平面把空间分成……(　 )

A、2部分　 B、3部分　 C、3部分或4部分　 D、2部分或3部分

22．(本题14分)设ΔABC和ΔDBC所在的两个平面互相垂直，且AB=BC=BD，

∠ABC=∠DBC=120⁰，

求：(1)直线AD与面BCD所成角的大小

A 　 　 B　　　　　　 C 　 　 　 D

(2)异面直线AD与BC所成的角

(3)　　　 二面角A-BD-C的大小。

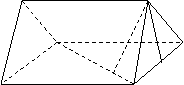
21．(本题12分)如图，直三棱柱ABC-A₁B₁C₁的侧棱AA₁=4cm，底面是等腰直角三角形，且AC=BC=2cm，∠C=90⁰，E为AB的中点，CD⊥AB₁

C1　　　　　　　　　　 C 　 　　 B1　　　　　　　　　　　　　　 　B 　　　　　　　　 D　　　　 E A1　　　　　　　　　　 A

(1)　 求异面直线CE与AB₁的距离

(2)　 求点E到平面ACB₁的距离

20．(本题满分12分)

一个口袋内装有4个不同的红球，6个不同的白球，若取出一个红球记2分，取出一个白球记1分. 问：从口袋中取5个球，使总分不小于7分的取法有多少种？

19．(本题12分)如图，ABCD是直角梯形，∠BAD=90⁰，∠SAB=90⁰，SA⊥面ABCD，SA=AB=BC=1，AD=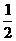，求面SCD与面SBA所成的二面角的正切值。

18．(本题满分12分)

(1)求证：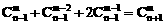

(2)设(1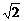－x)²⁰⁰²＝a₀+a₁x+a₂x²+……+a₂₀₀₂x²⁰⁰²，其中，a₀，a₁，a₂，…，a₂₀₀₂

是常数，求：(a₀+a₂+a₄+……+a₂₀₀₂)²－(a₁+a₃+a₅+……+a₂₀₀₁)² 的值.

S 　 　　　　 B　　　　 C 　 A　　　 D