
题目列表(包括答案和解析)
5. 四棱锥成为正棱锥的一个充分但不必要条件是 ( )
A.各侧面是正三角形 B.底面是正方形
C.各侧面三角形的顶角为45度 D.顶点到底面的射影在底面对角线的交点上
4. 在斜棱柱的侧面中,矩形最多有 ( )个。
A.2 B. 3 C.4 D.6
3. 正四棱锥的一个对角面与一个侧面的面积之比为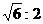 ,则侧面与底面的夹角为( )
,则侧面与底面的夹角为( )
A.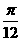 B.
B.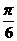 C.
C.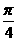 D.
D.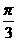
2. 设M、O、A、B、C是空间的点,则使M、A、B、C一定共面的等式是 ( )
A.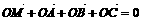 B.
B.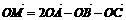
C.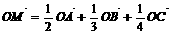 D.
D.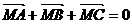
1.
已知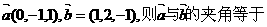 ( )
( )
A.90° B.30° C.60° D.150°
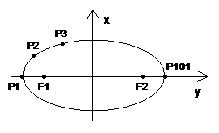
22.(本题满分18分)如图,已知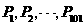 均是椭圆
均是椭圆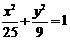 上的点,且P1,P101是长轴的两个端点,令
上的点,且P1,P101是长轴的两个端点,令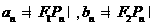 ,
,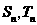 分别是数列{
分别是数列{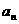 }和
}和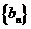 的前n项和。
的前n项和。
(1)若{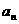 }是等差数列,求数列{
}是等差数列,求数列{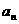 }的公差d及{
}的公差d及{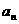 }和
}和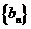 的通项公式;
的通项公式;
 (2对于(1)中数列{
(2对于(1)中数列{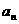 },当2
},当2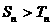 时,求n的取值范围;
时,求n的取值范围;
(3)若{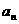 }是等比数列,令
}是等比数列,令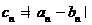 ,求数列
,求数列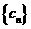 的最小值及此时n的取值。(精确到0.0001)
的最小值及此时n的取值。(精确到0.0001)
21.(本题满分16分)某市2000年底有100万人,人均住房面积为10 ,由于政策移民等因素,人口年平均增长6%,为了改善市民的住房条件,市政府规定:从2001年起,每年新建住房60万
,由于政策移民等因素,人口年平均增长6%,为了改善市民的住房条件,市政府规定:从2001年起,每年新建住房60万 ,若2001年记作第一年。
,若2001年记作第一年。
(1)写出第n年该市的人口总数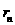 (万人)和住房总面积
(万人)和住房总面积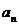 (万
(万 );
);
(2)计算2006年底该市的人均住房面积,该数据说明什么问题?(精确到0.1 )
)
(3)按照这种新房建设速度,到2008年底,若要实现本届市政府提出的“人均住房面积达到14 ”的目标,必须从2001起,将人口的增长率控制在多少以内?(精确到0.1%)
”的目标,必须从2001起,将人口的增长率控制在多少以内?(精确到0.1%)
20.(本题满分14分)已知点A(0,4),双曲线C: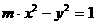 的渐近线经过点
的渐近线经过点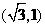 ,点P在双曲线的右支上。
,点P在双曲线的右支上。
(1)求|AP|的最小值及此时P点的坐标;
(2)设M,N是双曲线C上任意两点,线段MN的中点为B,若直线MN和直线OB的斜率存在,记为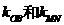 ,求证:
,求证: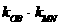 是个常数。
是个常数。
19.(本题满分14分)
已知椭圆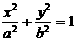 (a>b>0)上的点
(a>b>0)上的点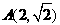 到两焦点的距离之和为
到两焦点的距离之和为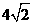 。
。
(1)求椭圆的方程;
(2)过椭圆右焦点,倾斜角为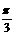 的直线与椭圆相交于P,Q两点,求线段|PQ|的长。
的直线与椭圆相交于P,Q两点,求线段|PQ|的长。
18.(本题满分12分)已知直线2x+y+4=0与圆C: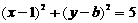 相切,圆C与x轴的负半轴交于A点,与y轴的正半轴交于B点,求
相切,圆C与x轴的负半轴交于A点,与y轴的正半轴交于B点,求 的值。(结果用反三角函数值表示)
的值。(结果用反三角函数值表示)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com