
题目列表(包括答案和解析)
21.已知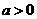 ,函数
,函数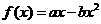
(1)当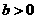 时,若对任意
时,若对任意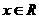 都有
都有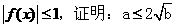
(2)当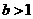 时,证明:对任意
时,证明:对任意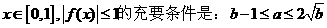
(3)当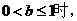 探讨:对
探讨:对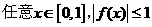 的充要条件(不必证明)。
的充要条件(不必证明)。
(答案0<a<1)
20.甲、乙两地相距s千米,汽车从甲地匀速行驶到乙地,速度不得超过c千米/时.已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v(千米/时)的平方成正比,且比例系数为b;固定部分为a元.
(Ⅰ)把全程运输成本y(元)表示为速度v(千米/时)的函数,并指出这个函数的定义域;
(Ⅱ)为了使全程运输成本最小,汽车应以多大速度行驶?
答案:(1)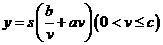 ,(2)当
,(2)当 时,
时,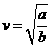 ,当
,当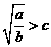 时,
时,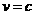
19.1,1,2,3,5,8,13, 这一数列的规律是:第1、第2个数是1,从第3个数起,该数是前面2个数的和。试用伪代码写出计算这个数列前30项和的算法,并画出流程图。
这一数列的规律是:第1、第2个数是1,从第3个数起,该数是前面2个数的和。试用伪代码写出计算这个数列前30项和的算法,并画出流程图。
18.(本题满分14分)设函数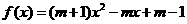
(1)若不等式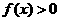 的解集为R,求实数m的取值范围。
的解集为R,求实数m的取值范围。
(2)若不等式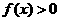 有解,求实数m的取值范围。
有解,求实数m的取值范围。
答案: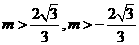
17.(本题满分14分)
(1)袋中有2个红球,2个白球,2个黑球,从中任意摸出2个球,求至少有1个红球的概率。
(2)用计算机随机产生的有序数组(x, y),满足-1 < x <1, -1 < y < 1,求数组(x, y)满足| x | - y > 0 的概率。
答案: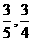
16.对任意实数a,b,c,给出下列命题:①“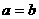 ”是“
”是“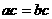 ”充要条件;②“
”充要条件;②“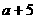 是无理数”是“a是无理数”的充要条件③“a>b”是“a2>b2”的充分不必要条件;④“a<5”是“a<3”的必要不充分条件。
是无理数”是“a是无理数”的充要条件③“a>b”是“a2>b2”的充分不必要条件;④“a<5”是“a<3”的必要不充分条件。
其中真命题的序号是______②_____④_________。
15.一组数据中的每一个数据都减去80,得到一组新数据的平均值是1.2,方差是4.4,则原数据的平均值和方差分别是 (81.2 , 4.4 )。
14.某公司一年购买某种货物400吨,每次都购买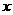 吨,运费为
吨,运费为
4万元/次,一年的总存储费用为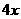 万元,要使一年的总运费与总
万元,要使一年的总运费与总
存储费用之和最小,则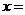 ( 20 )吨。
( 20 )吨。
13.函数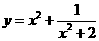 的值域为(
的值域为(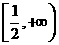 )。
)。
12.右边伪代码运行输出结果为___0,6______________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com