
题目列表(包括答案和解析)
5.若α是直线的倾斜角,则sin(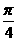 -α)的取值范围是( )
-α)的取值范围是( )
A.[-1,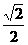 ] B.(-1,
] B.(-1,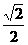 )
)
C.(- 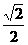 ,
,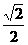 ) D.[-
) D.[-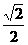 ,
,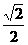 )
)
4.直线ax+by=ab(a>0,b<0)的倾斜角是( )
A.arctan(-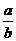 )
B.arctan
)
B.arctan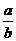
C.π-arctan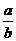 D.
D. 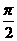 +arctan
+arctan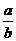
3.若三点A(3,1),B(-2,b),C(8,11)在同一直线上,则实数b等于( )
A.2 B.3 C.9 D.-9
2.若图中的直线l1、l2、l3的斜率分别为k1、k2、k3,则有( )
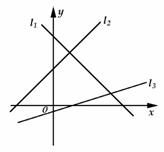
A.k1<k2<k3 B.k3<k1<k2 C.k3<k2<k1 D.k1<k3<k2
1.经过两点M(6,8)、N(9,4)的直线的倾斜角为( )
A.arctan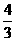 B.arccot
B.arccot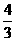
C.arctan(-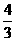 ) D.π-arctan
) D.π-arctan
5.北京华掀公司计划在今年内同时出售“夜莺牌多功能”电子琴和“OK智能型”洗衣机,由于两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大.已知对这两种产品有直接限制的因素是资金和劳动力,通过调查,得到关于两种产品有关数据如下表:
资金
单位产品所需资金
月资金供应量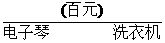 (百元) (百元) |
|
成本
30
20
300 |
|
劳动力(工资) 5
10
110 |
|
单位利润
6
8 |
试问:怎样确定两种货的供应量,才能使总利润最大,最大利润是多少?(14′)
4.P为直线l:Ax+By+c=0上一动点,M(a,b)为一定点,点Q在直线MP上,且MQ:QP=λ,求Q点轨迹(λ≠-1,λ≠0).(15′)
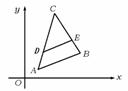
3.如图,△ABC中,DE∥AB,A(1,1),C(4,5)且S△CDE=S四边形ABED,求D点坐标.(12′)
2.已知△ABC三边所在直线方程是AB:4x-3y+10=0;BC:y-2=0;CA:3x-4y-5=0.求:(15′)
①∠B的大小;
②∠BAC内角平分线方程;
③AB边上的高所在直线方程.
1.已知A(1,2),B(5,4)和直线x-2y-2=0上一动点P,且点P使|PA|+|PB|最小,求点P的坐标.(12′)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com