
题目列表(包括答案和解析)
8.若抛物线y2=2px (p>0)上三点的纵坐标的平方成等差数列,那么
这三点的焦半径的关系为 ( A )
(A) 成等差数列 (B)成等比数列
(C) 既成等差数列又成等比数列 (D)既不成等差数列又不成等比数列
7.如果存在实数a,使cosa=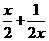 成立,那么实数x的集合是 ( A )
成立,那么实数x的集合是 ( A )
(A){-1.1}(B){x|x<0或x=1}(C) { x|x>0或x=-1}(D){x|x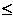 -1 或x
-1 或x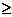 1}
1}
6.设椭圆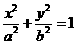 (a>b>0)的离心率为
(a>b>0)的离心率为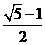 ,F,A分别是椭圆的左焦点,右顶点,B是它短轴的一个端点,则
,F,A分别是椭圆的左焦点,右顶点,B是它短轴的一个端点,则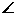 ABF 为
( C )
ABF 为
( C )
(A) 30 ° (B) 75° (C)90° (D) 120°
5.定义在R上的偶函数f(x)满足f(x+4)= -f(x),在[0,4]上
为减函数 ,则 ( B )
(A)f(10)<f(13)<f(15), (B)f(13)<f(10)<f(15)
(C)f(15)<f(10)<f(13) (D)f(15)<f(13)<f(10)
4. 过抛物线y2=4x的焦点作直线交抛物线于A(x1 , ,y1)B(x2, ,y2)两点,
若AB与x轴成45 ,则AB的长为
( B )
,则AB的长为
( B )
(A)10 ( B) 8 ( C) 6 ( D) 4
3. 奇函数y=f(x)在x 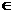 (0, +
(0, + )时,f(x)=x-1,则f(x-1)<0的解集为 ( B )
)时,f(x)=x-1,则f(x-1)<0的解集为 ( B )
(A){x|-1<x<0} (B){x|x<0,或1<x<2}
(C){x|0<x<2} (D){x|1<x<2}
2.a=1是直线x+ay=a+2与直线ax+y=2a+1平行的 ( D )
(A) 充要条件 (B) 充分不必要条件
(C) 必要不充分条件(D)既不充分也不必要条件
1.
A={x|x2-2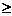 0}, B={x|x2-4x+3
0}, B={x|x2-4x+3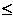 0},则A
0},则A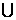 B=
( C )
B=
( C )
(A){x|x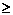
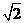 或x
或x  1} (B){x|x
1} (B){x|x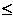
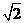 或x
或x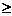 3}
3}
(C) {x|x
{x|x  -
-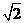 或x
或x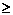 1} (D) R
1} (D) R
22.某房屋开发公司用128万元购得一块土地,欲建成不低于五层的楼房一幢,该楼每层的建筑面积为1000平方米,楼房的总建筑面积(即各层面积之和)的每平方米的平均建筑费用与楼层有关,若该楼建成x层时,每平方米的平均建筑费用用f(x)表示,且f(n)=f(m)(1+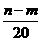 )(其中n>m,n∈N),又知建成五层楼房时,每平方米的平均建筑费用为400元,为了使该楼每平方米的综合费用最省(综合费用是建筑费用与购地费用之和),公司应把该楼建成几层?(13分)
)(其中n>m,n∈N),又知建成五层楼房时,每平方米的平均建筑费用为400元,为了使该楼每平方米的综合费用最省(综合费用是建筑费用与购地费用之和),公司应把该楼建成几层?(13分)
21.某工厂库存A、B、C三种原料,可用来生产甲、乙两种产品,市场调查显示其用料和可获利润等各数据如下表:
 原 料 原 料耗料 产品 |
A(吨) |
B(吨) |
C(吨) |
|
每吨产品利润(元) |
|
|
100 |
125 |
156 |
(I) |
(II) |
||
|
甲产品每1吨 |
1 |
2 |
3 |
|
2000 |
1000 |
|
乙产品每1吨 |
4 |
3 |
1 |
|
1000 |
3000 |
问:(1) 若市场情况如(I),怎样安排生产才能获得最大利润?
(2) 若市场情况如(II),怎样安排生产才能获得最大利润?(13分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com