10．如图，在四棱锥P－ABCD中，底面ABCD是平行四边形，PA⊥底面ABCD，且PA＝AD＝2a，AB＝a，AC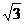＝a．

(1)求证：平面PDC⊥平面PAC；

(2)求异面直线PC与BD所成角的余弦值；

(3)设二面角A－PC－B的大小为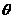，求tg．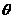

9．如图，在三棱锥P－ABC中，PA＝PC，∠APC＝∠ACB＝90°，∠BAC＝30°，平面PAC⊥平面ABC．

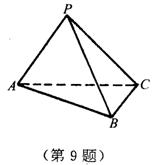
(1)求证：平面PAB⊥平面PBC；

(2)求二面角P－AB－C的大小；

(3)若PA＝2，求三棱锥P－ABC的体积．

8．如图△ABC是等腰直角三角形，AB＝BC＝4，△BCD是等边三角形，将它们折成直二面角A－BC－D．

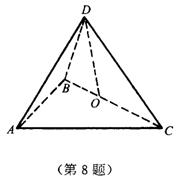
(1)取BC的中点O，证明：DO⊥面ABC；

(2)求二面角D－AB－C的大小；

(3)求AD与平面ABC所成角的正切；

(4)求AD与BC所成角的余弦．

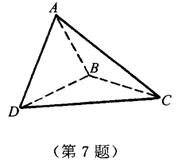
7．如图，△ABC与△BCD所在平面互相垂直，且AB＝BC＝BD，∠ABC＝∠DBC＝120°．求：

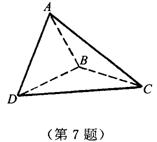
(1)直线AD与面BCD所成的角；

(2)直线AD与BC所成的角；

(3)二面角A－BD－C的大小．

6．正三棱锥P－ABC的高和底面边长都等于a，EF是PA与BC的公垂线，E，F分别为垂足．

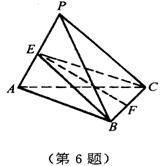
(1)求证：侧棱PA⊥截面BEC；

(2)求截面BEC的面积；

(3)求截面BEC与底面ABC所成二面角的大小．

5．已知四棱锥P－ABCD，它的底面ABCD是边长为a的菱形，且∠ABC＝120°，PC⊥面ABCD．又PC＝a，E为PA的中点．

(1)求证：面EBD⊥面ABCD；

(2)求点E到平面PBC的距离；

(3)求二面角A－BE－D的大小．

4．AB是Rt△ABC的斜边，P是平面ABC外的一点，且P到△ABC的三个顶点的距离相等．求证：平面PAB⊥平面ABC．

3．ABCD是空间四边形，H，F分别是AC，BD，过H，F且平行于AD的平面分别交AB，CD于E，G．求证：BC∥面EFGH．

2．在四面体ABCD中，AC⊥BD，AH⊥面BCD，H为垂足，CK⊥面ABD，K为垂足．求证：AH与CK必相交．

1．在正方体，ABCD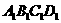－中，E，F，G，H，M，N分别是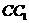，BC，AB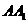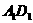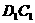，，，的中点，求证：这些中点共面．