
20.(本小题满分16分)
已知△OFQ的面积为2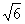 ,且
,且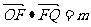 .
.
(1)若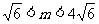 ,求向量
,求向量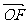 与
与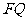 的夹角
的夹角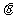 的取值范围;
的取值范围;
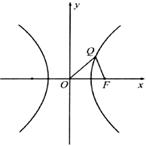
(2)设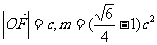 时,若以O为中心,F为焦点的双曲线经过点Q(如图),当
时,若以O为中心,F为焦点的双曲线经过点Q(如图),当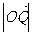 取得最小值时,求此双曲线的方程.
取得最小值时,求此双曲线的方程.
19.(本小题满分16分)
已知数列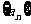 中,
中,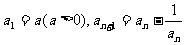 .
.
(1)若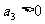 ,求实数
,求实数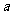 的取值范围;
的取值范围;
(2)是否存在正实数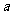 ,使
,使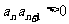 对任意
对任意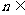 N*恒成立.如果存在,请求出
N*恒成立.如果存在,请求出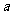 的值; 如果不存在,请说明理由.
的值; 如果不存在,请说明理由.
18.(本小题满分16分)
正三棱柱ABC-A1B1C1的所有棱长都是2,D是棱AC的中点,E是棱CC1的中点,AE交A1D于点H.
(1)求证:AE⊥平面A1BD;
(2)求二面角D-BA1一A的大小(用反三角函数表示结果);
(3)求点B1到平面A1BD的距离.
17.(本小题满分14分)
设向量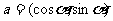 ,
,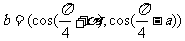 ,
,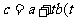 ∈R),其中
∈R),其中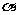 为锐角.
为锐角.
(1)求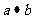 ;
;
(2)当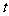 为何值时,c的模最小?最小值是多少?
为何值时,c的模最小?最小值是多少?
16.在直三棱柱A1BlC1-ABC中,∠BAC=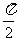 ,AB=AC=AA1=1.已知G与E分别为A1B1和CC1的中点,D与F分别为线段AC和AB上的动点(不包括端点).若GD⊥EF,则线段DF的长度的取值范围为 ( )
,AB=AC=AA1=1.已知G与E分别为A1B1和CC1的中点,D与F分别为线段AC和AB上的动点(不包括端点).若GD⊥EF,则线段DF的长度的取值范围为 ( )
A.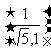 B.
B.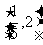 C.
C.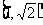 D.
D.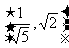
15.设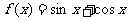 ,下列命题:①
,下列命题:① 既不是奇函数,又不是偶函数;②若
既不是奇函数,又不是偶函数;②若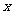 是三角形内角,则
是三角形内角,则 是增函数;③若
是增函数;③若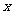 是三角形内角,则
是三角形内角,则 有最大值,无最小值;
④
有最大值,无最小值;
④ 的最小正周期为
的最小正周期为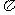 ,其中正确命题的序号是 ( )
,其中正确命题的序号是 ( )
A.①② B.①③ C.②③ D.②④
14.将棱长为3的正四面体的各棱长三等分,经过分点将原正四面体各顶点附近均截去 一个棱长为1的小正四面体,则剩下的多面体的棱数E为 ( )
A.16 B.17 C.18 D.19
13.函数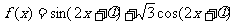 的图像关于原点对称的充要条件是( )
的图像关于原点对称的充要条件是( )
A.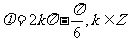 B.
B.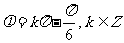
C.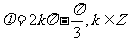 D.
D.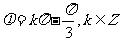
12.某车站,每天均有3辆客车开往省城,客车分为上、中、下三个等级.某人准备在该车站乘车前往省城办事,但他不知道客车的车况,也不知道发车顺序.为了尽可能乘上上等车,他将采取如下策略:先放过第一辆,如果第二辆比第一辆好,则上第二辆;否则,上第三辆.那么他乘上上等车的概率为 .
11.设ABCD一AlBlClDl是一个正方体,点M是棱AA1的中点,则二面角B1一MC-A1的大小是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com