
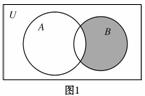
3.如图1所示,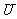 是全集,
是全集,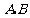 是
是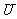 的子集,则阴影部分所表示的集合是
的子集,则阴影部分所表示的集合是
A.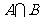 B.
B.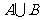 C.
C.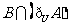 D.
D.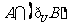
2. 点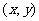 在映射
在映射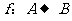 作用下的象是
作用下的象是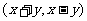 ,则点
,则点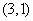 在
在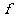 的作用下的原象是
的作用下的原象是
A.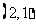 B.
B.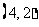 C.
C.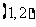 D.
D.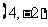
1. 集合A={a, b}的真子集的个数是
A.1 B.2 C.3 D.4
21.(本小题满分18分)
已知数列{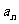 }满足
}满足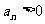 ,且对一切
,且对一切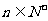 ,有
,有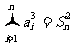 ,其中
,其中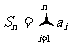 。
。
(1)求证:对一切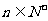 ,有
,有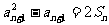 ;
;
(2)求数列{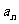 }的通项公式;
}的通项公式;
(3)求证: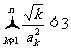
20.(本小题满分16分)
已知 ,函数
,函数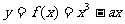 在[1,+∞)上是一个单调函数。
在[1,+∞)上是一个单调函数。
(1)试问函数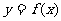 在
在 的条件下,在[1,+∞)上能否是单调递减函数?请说明理由;
的条件下,在[1,+∞)上能否是单调递减函数?请说明理由;
(2)若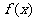 在区间[1,+∞)上是单调递增函数,试求出实数
在区间[1,+∞)上是单调递增函数,试求出实数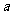 的取值范围;
的取值范围;
(3)设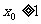 ,
,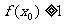 1且
1且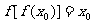 ,求证:
,求证: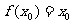 。
。
19.(本小题满分16分)
已知直四棱柱ABCD-A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1的中点,M为线段AC1的中点。
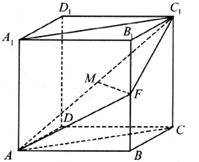
(1)求证:直线MF∥平面ABCD;
(2)求证:平面AFC1⊥平面ACC1A1;
(3)求平面AFC1与平面ABCD所成二面角的大小。
18.(本小题满分16分)
设函数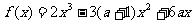 ,
,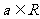
(1)当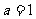 时,试用单调性的定义证明
时,试用单调性的定义证明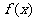 为单调增函数;
为单调增函数;
(2)当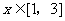 时,
时,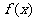 的最小值为4,求
的最小值为4,求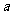 的值。
的值。
17.(本小题满分14分)
已知点A(-2,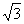 ),F是椭圆
),F是椭圆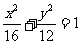 的右焦点,点M在椭圆上移动,当
的右焦点,点M在椭圆上移动,当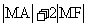 取最小值时,求点M的坐标。
取最小值时,求点M的坐标。
16.有一个正四棱锥,它的底面边长与侧棱长均为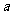 ,现用一张正方形包装纸将其完全包住(不能裁剪纸,但可以折叠),那么包装纸的最小边长应为
,现用一张正方形包装纸将其完全包住(不能裁剪纸,但可以折叠),那么包装纸的最小边长应为
A.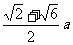 B.
B.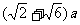 C.
C.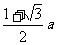 D.
D.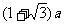
15.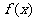 是定义在实数集R上的奇函数,且
是定义在实数集R上的奇函数,且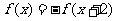 ,当
,当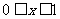 时,
时,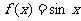 ,则使
,则使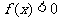 成立的
成立的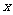 的取值范围是
的取值范围是
A.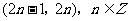 B.
B.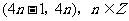
C.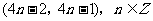 D.
D.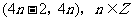
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com