
21.(本大题满分14分)
设定义在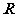 上的函数
上的函数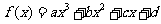 同时满足下列三个条件:
同时满足下列三个条件:
①函数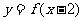 的图象关于点
的图象关于点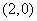 对称
对称
②函数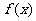 的图象过点
的图象过点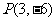
③函数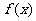 在
在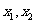 处取得极值,且
处取得极值,且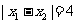
⑴求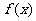 的表达式;
的表达式;
⑵求过点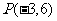 与函数
与函数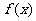 的图象相切的直线方程。
的图象相切的直线方程。
20.(本大题满分13分)
已知椭圆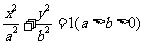 的中心在坐标原点
的中心在坐标原点 ,一条准线的方程为
,一条准线的方程为 ,过椭圆的左焦点
,过椭圆的左焦点 ,且方向向量为
,且方向向量为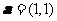 的直线
的直线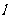 交椭圆于
交椭圆于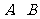 两点,
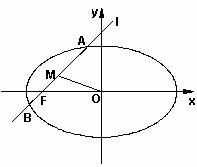
两点,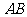 的中点为
的中点为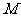
⑴求直线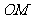 的斜率(用
的斜率(用 表示);
表示);
⑵设直线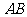 与
与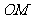 的夹角为
的夹角为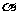 ,当
,当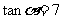 时,求椭圆的方程。
时,求椭圆的方程。
19.(本大题满分12分)
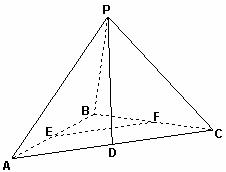
如图:在三棱锥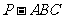 中,
中,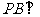 面
面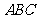 ,
,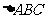 是直角三角形,
是直角三角形,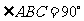 ,
,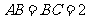 ,
,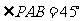 ,点
,点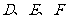 分别为
分别为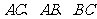 的中点。
的中点。
⑴求证: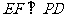 ;
;
⑵求直线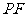 与平面
与平面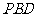 所成的角的大小;
所成的角的大小;
⑶求二面角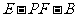 的正切值。
的正切值。
18.(本大题满分12分)
已知数列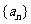 中,
中,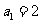 ,前
,前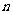 项和为
项和为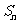 ,对于任意
,对于任意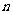 ≥
≥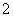 时,
时,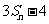 ,
,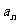 ,
,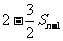 总成等差数列。
总成等差数列。
⑴求数列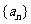 的通项公式;
的通项公式;
⑵若数列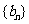 满足
满足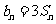 ,求数列
,求数列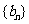 的前
的前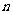 项和
项和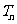
17.(本大题满分12分)
如图是一个方形迷宫,甲、乙两人分别位于迷宫的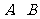 两处,两人同时以每一分钟一格的速度向东、西、南、北四个方向行走,已知甲向东、西行走的概率都为
两处,两人同时以每一分钟一格的速度向东、西、南、北四个方向行走,已知甲向东、西行走的概率都为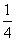 ,向南、北行走的概率为
,向南、北行走的概率为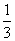 和
和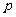 ,乙向东、西、南、北四个方向行走的概率均为
,乙向东、西、南、北四个方向行走的概率均为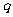
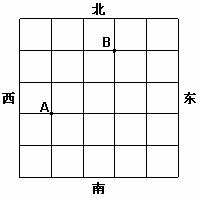
⑴求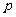 和
和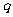 的值;
的值;
⑵问最少几分钟,甲、乙二人相遇?并求出最短时间内可以相遇的概率。
16.(本大题满分12分)
已知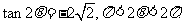
⑴求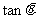 值;
值;
⑵求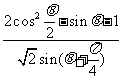 的值
的值
15.定义在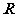 上的函数
上的函数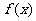 :当
:当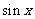 ≤
≤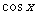 时,
时,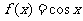 ;当
;当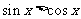 时,
时,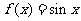 。给出以下结论:
。给出以下结论:
①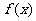 是周期函数
是周期函数
②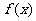 的最小值为
的最小值为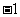
③当且仅当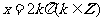 时,
时,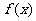 取最大值
取最大值
④当且仅当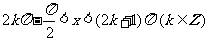 时,
时,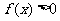
⑤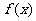 的图象上相邻最低点的距离是
的图象上相邻最低点的距离是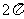
其中正确命题的序号是 (把你认为正确命题的序号都填上)
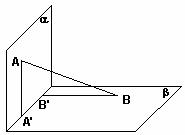
14.如图,平面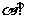 平面
平面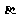 ,
,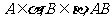 与平面
与平面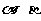 所成的角分别为
所成的角分别为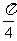 和
和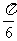 ,过
,过 分别作两平面交线的垂线,垂足为
分别作两平面交线的垂线,垂足为 ,则
,则 。
。
13.已知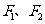 分别为双曲线
分别为双曲线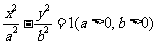 的左右焦点,
的左右焦点,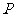 为双曲线左支上的一点,若
为双曲线左支上的一点,若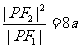 ,则双曲线的离心率的取值范围是
。
,则双曲线的离心率的取值范围是
。
12.不等式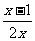 ≤
≤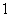 的解集是
的解集是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com