
6.要从10名女生和5名男生中选出6名学生组成课外学习小组,如果按性别依比例分层随机抽样,试问组成此课外学习小组的概率为 ( )
A.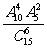 B.
B.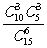 C.
C.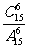 D.
D.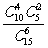
5.一个容量为20的样本数据,分组后,组距与频数如下: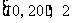 ;
;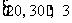 ;
;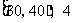 ;
;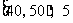 ;
;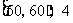 ;
;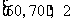 . 则样本在区间
. 则样本在区间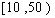 内的频率是 ( )
内的频率是 ( )
A.0.25 B.0.50 C.0.70 D.0.75
4.现有男生3人,女生5人,从男生中选2人,从女生中选1人分别参加数学、物理、化学三科竞赛,那么不同的方案为 ( )
A.90 B.45 C.30 D.15
3.函数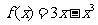 的递增区间是 ( )
的递增区间是 ( )
A. B.
B.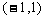 C.
C.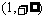 D.
D. ,
,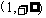
2.有四位司机,四位售票员分配到四辆公共汽车上,使每辆车分别有一位司机和一名售票员,则可能的分配方案数是 ( )
A.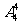
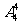 B.
B.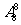 C.
C.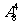 D.
D.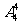
1.曲线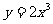 在
在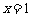 处的切线的斜率是 ( )
处的切线的斜率是 ( )
A.2 B.4 C.6 D.8
22.(本小题满分14分)
已知曲线C: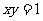 ,过C上一点A
,过C上一点A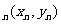 作一斜率为
作一斜率为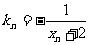 的直线交曲线C于另一点A
的直线交曲线C于另一点A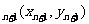 ,点列A
,点列A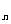 (n=1,2,3,…)的横坐标构成数列{
(n=1,2,3,…)的横坐标构成数列{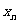 },其中
},其中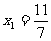 .
.
(Ⅰ)求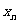 与
与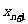 的关系式;
的关系式;
(Ⅱ)求证: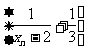 是等比数列;
是等比数列;
(Ⅲ)求证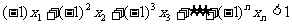 .(n∈N,n≥1)
.(n∈N,n≥1)
21.(本小题满分12分)
已和直线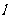 :
: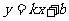 与椭圆
与椭圆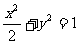 相交于A、B两点,O为坐标原点.
相交于A、B两点,O为坐标原点.
(Ⅰ)当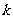 =0,0<b<1时,求△AOB的面积S的最大值;
=0,0<b<1时,求△AOB的面积S的最大值;
(Ⅱ)若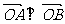 ,求证直线
,求证直线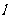 与以原点为圆心的定圆相切,并求该圆的方程.
与以原点为圆心的定圆相切,并求该圆的方程.
20.(本小题满分12分)
已知函数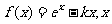 ∈R.
∈R.
(Ⅰ)试确定函数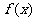 的单调区间;
的单调区间;
(Ⅱ)若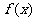 在区间(0,2)内恰好有两个零点,求实数
在区间(0,2)内恰好有两个零点,求实数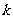 的取值范围.
的取值范围.
19.(本小题满分12分)
某学校对高三(1)班的50位同学进行成绩分析,随机抽取8位同学的数学,物理试卷,将他们的数学成绩从小到大排序分别是:60,65,70,75,80,85,90,95,物理成绩从小到大排序分别是:72,77,80,84,88,90,93,95.
(Ⅰ)若规定85分以上(含85分)为优秀,求这8位同学中恰有3位同学的数学成绩和物理成绩均优秀的概率;
(Ⅱ)若这8位同学的数学,物理成绩事实上对应于下表:
|
学生编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
数学成绩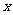 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
物理成绩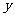 |
72 |
77 |
80 |
84. |
88 |
90 |
93 |
95 |
利用散点图判断物理成绩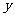 与数学成绩
与数学成绩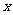 之间是否具有相关关系?若具有相关关系,求出
之间是否具有相关关系?若具有相关关系,求出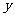 与
与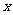 的线性回归方程(系数精确到0.01);否则,说明理由;
的线性回归方程(系数精确到0.01);否则,说明理由;
(Ⅲ)若某同学的数学成绩为72分,请你预测该同学的物理成绩.
参考数据: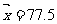 ,
,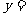 =85,
=85,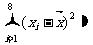 1050,
1050,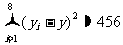 ,
,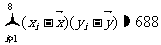 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com