
20.(本小题满分13分)
我国是水资源比较贫乏的国家,一些缺水的地区采用价格调控的手段来达到节约用水的目的。某市自来水收费采取的是分段收费的方法:用水不超过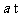 的每吨2元;用水超过
的每吨2元;用水超过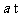 而不超过
而不超过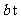 的,超过
的,超过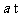 的部分每吨4元;用水超过
的部分每吨4元;用水超过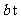 的,则超出
的,则超出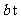 的部分每吨6元;另外,每户每月收定额损耗费
的部分每吨6元;另外,每户每月收定额损耗费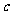 元,已知
元,已知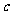 c超过5元。该市一家庭今年第一季度的用水量和支付费用如下表所示:
c超过5元。该市一家庭今年第一季度的用水量和支付费用如下表所示:
|
月份 |
用水量 |
支付费用 |
|
l |
15 |
42 |
|
2 |
2l |
68 |
|
3 |
8 |
18 |
根据上表中的数据,求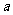 ,
,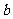 ,
,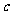 的值,并写出用水量
的值,并写出用水量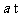 与支付费
与支付费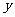 元的函数关系。
元的函数关系。
19.(本小题满分13分)
设G、M分别为不等边△ABC的重心与外心,A(-1,0)、B(1,0),且GM∥AB。
(1)求点C的轨迹E的方程;
(2)是否存在直线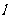 ,使
,使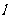 过点(0,1)并与曲线E交于P、Q两点,且满足OP⊥OQ?若存在,求出直线
过点(0,1)并与曲线E交于P、Q两点,且满足OP⊥OQ?若存在,求出直线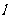 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
17.(本小题满分12分)
(理)如下图 a 所示,直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,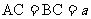 ,AA1=AB,E是AB1上的点。
,AA1=AB,E是AB1上的点。
(1)求二面角B1-AC-B的平面角的正切值;
(2)如何确定点E的位置,使得CE⊥AB1?并求此时C、E两点的距离。
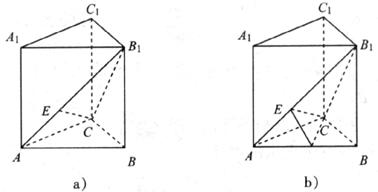
(文)如上图b所示,直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,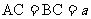 ,AA1=AB,C点在AB1上的射影为E,D为AB的中点。
,AA1=AB,C点在AB1上的射影为E,D为AB的中点。
(1)求证:AB1⊥平面CED;
(2)求二面角B1-AC-B的平面角的正切值。
16.(本小题满分12分)
已知函数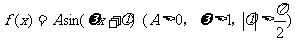 的部分图像如下图所示。
的部分图像如下图所示。
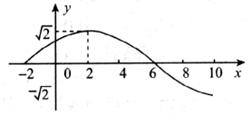
(1)求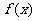 的解析式;
的解析式;
(2)(理)函数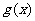 的图像与
的图像与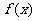 的图像关于点P(4,0)对称,求
的图像关于点P(4,0)对称,求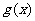 的单调递增区间。
的单调递增区间。
(文)写出函数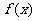 的单调递增区间。
的单调递增区间。
15.(理)已知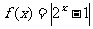 ,则方程
,则方程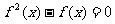 的不相等的实根共有 个。
的不相等的实根共有 个。
(文)方程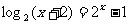 的实数解的个数是 个。
的实数解的个数是 个。
14.已知向量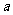 、
、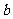 满足:
满足: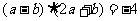 ,且
,且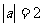 ,
,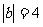 ,则
,则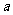 与
与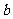 的夹角等于 。
的夹角等于 。
13.如果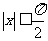 ,
,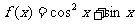 的最小值是 。
的最小值是 。
12.在数列{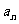 }中,其前
}中,其前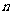 项和
项和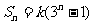 ,且
,且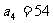 ,则
,则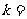 。
。
11.(理)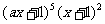 展开式中
展开式中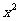 的系数为21,则
的系数为21,则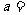 。
。
(文)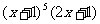 展开式中
展开式中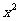 的系数为 。
的系数为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com