
20.(本大题满分13分)
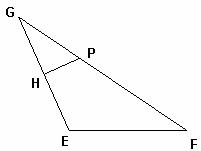
如图,已知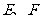 为平面上的两个定点,
为平面上的两个定点,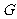 为动点,
为动点,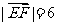 ,
,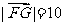 且
且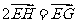 ,
,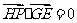 (
(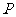 是
是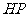 和
和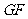 的交点)
的交点)
⑴建立适当的平面直角坐标系求出点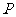 的轨迹方程;
的轨迹方程;
⑵若点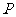 的轨迹上存在两个不同的点
的轨迹上存在两个不同的点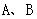 ,且线段
,且线段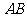 的中垂线与
的中垂线与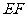 (或
(或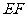 的延长线)相交于一点
的延长线)相交于一点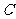 ,证明:
,证明: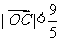 (
(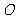 为
为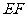 的中点)
的中点)
19.(本大题满分12分)
设函数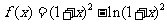
⑴求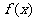 的单调区间;
的单调区间;
⑵若关于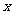 的方程
的方程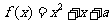 在区间
在区间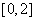 上恰有两个相异实根,求实数
上恰有两个相异实根,求实数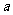 的取值范围。
的取值范围。
18.(本大题满分12分)
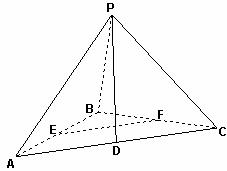
如图:在三棱锥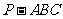 中,
中,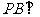 面
面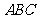 ,
,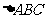 是直角三角形,
是直角三角形,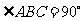 ,
,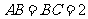 ,
,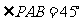 ,点
,点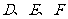 分别为
分别为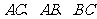 的中点。
的中点。
⑴求证: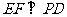 ;
;
⑵求直线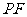 与平面
与平面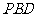 所成的角的大小;
所成的角的大小;
⑶求二面角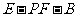 的正切值。
的正切值。
17.(本大题满分12分)
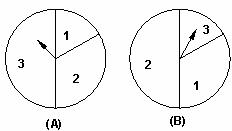
如图是两个独立的转盘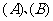 ,在两个图中三个扇形区域的圆心角分别为
,在两个图中三个扇形区域的圆心角分别为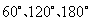 。用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘
。用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘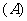 指针所对的区域数为
指针所对的区域数为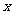 ,转盘
,转盘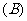 指针所对的区域为
指针所对的区域为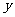 ,
,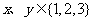 ,设
,设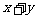 的值为
的值为 ,每一次游戏得到奖励分为
,每一次游戏得到奖励分为
⑴求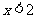 且
且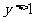 的概率;
的概率;
⑵某人进行了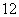 次游戏,求他平均可以得到的奖励分
次游戏,求他平均可以得到的奖励分
(注:这是一个几何概率题,几何概率的基本思想是把事件与几何区域对应,利用几何区域的度量来计算事件发生的概率,即事件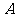 的概率
的概率 )
)
16.(本大题满分12分)
在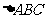 中,角
中,角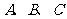 的对边分别为
的对边分别为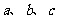 ,
,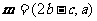 ,
,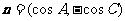 ,且
,且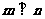 。
。
⑴求角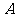 的大小;
的大小;
⑵当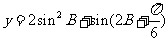 取最大值时,求角
取最大值时,求角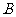 的大小
的大小
15.正三角形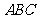 的边长为
的边长为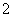 ,将它沿高
,将它沿高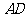 翻折成直二面角
翻折成直二面角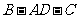 ,则三棱锥
,则三棱锥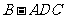 的外接球的表面积为
。
的外接球的表面积为
。
14.某仪器显示屏上的每个指示灯均以红光或蓝光来表示不同的信号,已知一排有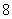 个指示灯,每次显示其中的
个指示灯,每次显示其中的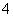 个,且恰有
个,且恰有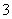 个相邻的。则一共显示的不同信号数是 。
个相邻的。则一共显示的不同信号数是 。
13.已知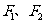 分别为双曲线
分别为双曲线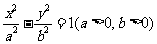 的左右焦点,
的左右焦点,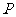 为双曲线左支上的一点,若
为双曲线左支上的一点,若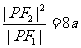 ,则双曲线的离心率的取值范围是
。
,则双曲线的离心率的取值范围是
。
12.在等差数列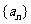 中,若
中,若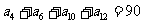 ,则
,则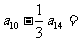 。
。
11.若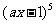 的展开式中
的展开式中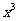 的系数是
的系数是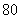 ,则实数
,则实数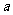 的值是 。
的值是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com