
6.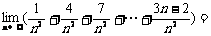 ( )
( )
A.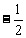 B.0 C.1 D.
B.0 C.1 D.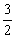
5.将容量为100的样本数据,分成8组,如下表:
|
组号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
频数 |
9 |
14 |
14 |
13 |
12 |
x |
13 |
10 |
则第6组的频率为 ( )
A.0.14 B.14 C.0.15 D.15
4.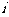 是虚数单位,
是虚数单位,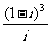 = ( )
= ( )
A.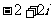 B.
B.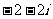 C.
C.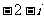 D.
D.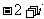
3.某个命题与正整数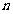 有关. 如果当
有关. 如果当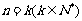 时该命题成立,那么可推得当
时该命题成立,那么可推得当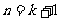 时该命题也成立. 现已知当
时该命题也成立. 现已知当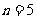 时该命题不成立,那么可推得 ( )
时该命题不成立,那么可推得 ( )
A.当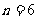 时该命题不成立 B.当
时该命题不成立 B.当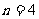 时该命题不成立
时该命题不成立
C.当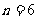 时该命题成立 D.当
时该命题成立 D.当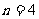 时该命题成立
时该命题成立
2.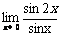 的值是 ( )
的值是 ( )
A.2 B.1 C.0 D.不存在
1.用数学归纳法证明: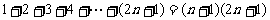 ,在验证
,在验证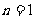 时等式成立时,等式的左边的式子是 ( )
时等式成立时,等式的左边的式子是 ( )
A.1 B.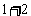 C.
C.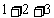 D.
D.
21.某人连续做同样的试验,每次试验只有成功与失败两种结果,已知第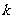 次成功时,第
次成功时,第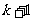 次成功的概率为
次成功的概率为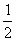 ;第
;第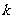 次失败时,第
次失败时,第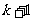 次成功的概率为
次成功的概率为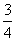 . 已知第2次试验成功的概率为
. 已知第2次试验成功的概率为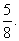
(Ⅰ)求第1次试验时成功的概率;
(Ⅱ)求第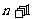 次试验成功的概率
次试验成功的概率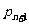 与第
与第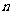 次试验成功的概率
次试验成功的概率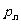 之间关系的表达式;
之间关系的表达式;
(Ⅲ)又假设如果试验成功,则停止试验,否则继续试验直至成功,试求恰好试验4次的概率.
22.已知函数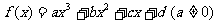 的图象经过原点,
的图象经过原点,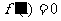 ,若
,若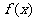 在
在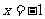 取得极大值2.
取得极大值2.
(Ⅰ)求函数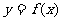 的解析式;
的解析式;
(Ⅱ)若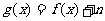 ,问是否存在实数
,问是否存在实数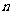 ,使得
,使得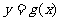 的图象与
的图象与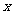 轴的图象有且只有一个交点?若存在,求出实数
轴的图象有且只有一个交点?若存在,求出实数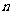 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(Ⅲ)若对任意的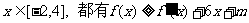 ,求实数
,求实数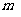 的最大值.
的最大值.
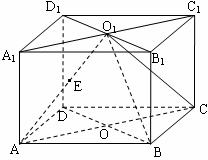
20.如图,直四棱柱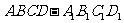 的高为3,∠DAB=60º,底面是边长为4的菱形,
的高为3,∠DAB=60º,底面是边长为4的菱形,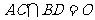 ,
,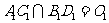 ,E是
,E是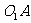 的中点.
的中点.
(Ⅰ)求二面角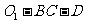 的大小;
的大小;
(Ⅱ)求点E到平面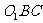 的距离.
的距离.
19.同时抛掷两个骰子(各个面上分别标以数字1,2,3,4,5,6),计算:
(Ⅰ)向上的数之和是7的概率;
(Ⅱ)向上的数之积为偶数的概率.
18.如图所示,已知直三棱柱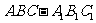 中,
中,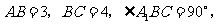 AA1=2.
AA1=2.
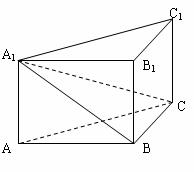
(Ⅰ)求证:平面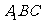 ⊥平面
⊥平面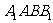 ;
;
(Ⅱ)求异面直线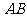 与
与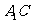 所成角的余弦值.
所成角的余弦值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com