3．函数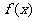为奇函数且周期为3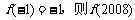，等于　　　　　　　　　　　　　　　 (　　 )

　　　 A．0　　　　　　　　　　　　 B．1　　　　　　　　　　　　 C．－1　　　　　　　　　　 D．2

2．设命题p：x<－1或x>1；命题q：x<－2或x>1，则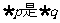的　　　　　　　　　　　 (　　 )

　　　 A．充分不必要条件　　　　　　　　　　　　　　　　 B．必要不充分条件

　　　 C．充要条件　　　　　　　　　　　　　　　　　　　　　 D．既不充分也不必要条件

1．设U=Z，A={1，3，5，7，9}，B={1，2，3，4，5}，则图中阴影部分表示的集合是　　　　　 (　　 )

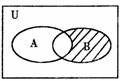
　　　 A．{1，3，5}　　　　　 B．{1，2，3，4，5}

　　　 C．{7，9}　　　　　　　 D．{2，4}

22．(本小题满分14分)

已知向量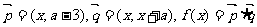，且m，n是方程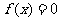的两个实根.

　 (Ⅰ)求实数a的取值范围；

　 (Ⅱ)设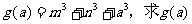的最小值；

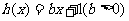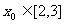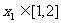　 (Ⅲ)给定函数，若对任意的，总存在，使得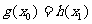，求实数b的取值范围.

21．(本小题满分12分)

某公司生产的A型商品通过租赁柜台进入某商场销售. 第一年，商场为吸引厂家，决定免收该年管理费，因此，该年A型商品定价为每件70元，年销售量为12.7万件. 第二年，商场开始对该商品征收比率为m%的管理费(即销售100元要征收m元)，于是该商品每件的定价提高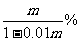，预计年销售量将减少m万件.

　 (Ⅰ)将第二年商场对该商品征收的管理费y(万元)表示成m的函数，并指出这个函数的定义域；

　 (Ⅱ)要使第二年商场在此项经营中收取的管理费不少于21万元，则商场对该商品征收管理费的比率m%的范围是多少？

　 (Ⅲ)第二年，商场在所收管理费不少于21万元的前提下，求使厂家获得最大销售金额时的m的值.

20．(本小题满分12分)

设数列{a_n}的前n项和S_n，且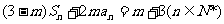. 其中m为常数，且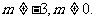

　 (Ⅰ)求证{a_n}是等比数列；

　 (Ⅱ)若数列{a_n}的公比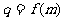，数列{b_n}满足

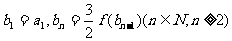，求证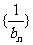为等差数列，并求b_n.

19．(本小题满分12分)

已知函数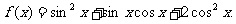

　 (Ⅰ)求函数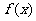的最值与最小正周期；

　 (Ⅱ)求使不等式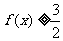成立的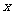的取值范围.

18．(本小题满分12分)

设函数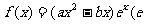为自然对数的底数)的图象与直线ex+y=0相切于点A，且点A的横坐标为1.

　 (Ⅰ)求a，b的值；

　 (Ⅱ)求函数f(x)的单调区间，并指出在每个区间上的增减性.

17．(本小题满分12分)

在△ABC中，a、b、c分别为角A、B、C的对边. 已知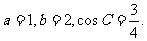

　 (Ⅰ)求边c的值；

　 (Ⅱ)求sin(C－A)的值.

16．若二次函数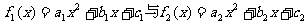满足下列条件：

　 (1)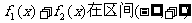上是单调减函数；

　 (2)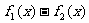在R上有最大值；

　　 则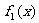与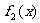的表达式可以是=　　　　　 ，=　　　　　　

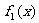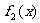(只要写出一组满足条件的表达式即可)