
20.(本小题满分12分)
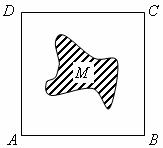
如图,面积为S的正方形ABCD中有一个不规则的图形M,可按下面方法估计M的面积:在正方形ABCD中随机投掷n个点,若n个点中有m个点落入M中,则M的面积的估计值为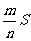 ,假设正方形ABCD的边长为2,M的面积为1,并向正方形ABCD中随机投掷10000个点,以X表示落入M中的点的数目。
,假设正方形ABCD的边长为2,M的面积为1,并向正方形ABCD中随机投掷10000个点,以X表示落入M中的点的数目。
(Ⅰ)求X的均值EX;
(Ⅱ)求用以上方法估计M的面积时,M的面积的估计值与实际值之差在区间(-0.03,,0.03)内的概率。
附表: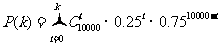
|
K |
2424 |
2425 |
2574 |
2575 |
|
P(k) |
0.0403 |
0.0423 |
0.9570 |
0.9590 |
19.(本小题满分12分)
在平面直角坐标系xOy中,经过点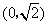 且斜率为k的直线l与椭圆
且斜率为k的直线l与椭圆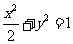 有两个不同的交点P和Q。
有两个不同的交点P和Q。
(Ⅰ)求k的取值范围;
(Ⅱ)设椭圆与x轴正半轴、y轴正半轴的交点分别为A、B,是否存在常数k,使得向量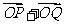 与
与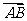 共线?如果存在,求k值;如果不存在,请说明理由。
共线?如果存在,求k值;如果不存在,请说明理由。
18.(本小题满分12分)
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,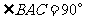 ,O为BC中点。
,O为BC中点。
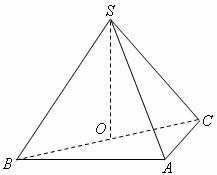
(Ⅰ)证明: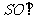 平面ABC;
平面ABC;
(Ⅱ)求二面角A-SC-B的余弦值。
17.(本小题满分12分)
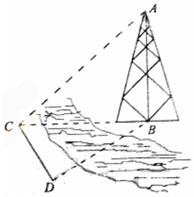
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D。现测得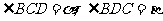 ,CD=s,并在点C测得塔顶A的仰角为
,CD=s,并在点C测得塔顶A的仰角为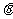 ,求塔高AB。
,求塔高AB。
16.某校安排5个班到4个工厂进行社会实践,每个班去一个工厂,每个工厂至少安排一个班,不同的安排方法共有 种。(用数字作答)
15.i是虚数单位,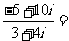 。(用a + bi的形式表示,
。(用a + bi的形式表示,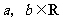 )
)
14.设函数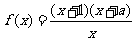 为奇函数,则a = 。
为奇函数,则a = 。
13.已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,则该双曲线的离心率为 。
12.一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱,这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等。设四棱锥、三棱锥、三棱柱的高分别为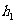 ,
,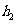 ,
,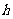 ,则
,则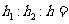 ( )
( )
A.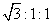
B.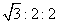
C.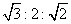
D.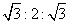
第Ⅱ卷
本卷包括必考题和选考题两部分,第13题-第21题为必考题,每个试题考生都必须做答,第22题为选考题,考生根据要求做答。
11.甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表
|
甲的成绩 |
||||
|
环数 |
7 |
8 |
9 |
10 |
|
频数 |
5 |
5 |
5 |
5 |
|
乙的成绩 |
||||
|
环数 |
7 |
8 |
9 |
10 |
|
频数 |
6 |
4 |
4 |
6 |
|
丙的成绩 |
||||
|
环数 |
7 |
8 |
9 |
10 |
|
频数 |
4 |
6 |
6 |
4 |
s 1,s 2,s 3分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( )
A.s 3>s 1>s 2
B.s 2>s 1>s3
C.s 1>s 2>s3
D.s 2>s3>s1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com