
6.已知圆O的半径为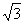 ,圆周上两点A、B与原点O恰构成三角形,则向量
,圆周上两点A、B与原点O恰构成三角形,则向量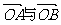 的数量积是 ( )
的数量积是 ( )
A.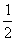 B.
B.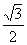 C.
C.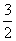 D.
D.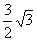
5.若等差数列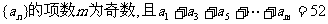
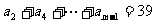 则m= ( )
则m= ( )
A.3 B.5 C.7 D.9
4.偶函数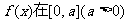 上是单调函数,且
上是单调函数,且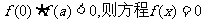 在
在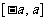 ,内根的个数是 ( )
,内根的个数是 ( )
A.1个 B.2个 C.3个 D.0个
3.已知函数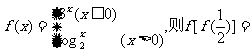 ( )
( )
A.-1 B.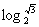 C.
C.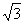 D.
D.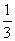
2.若 的值是 ( )
的值是 ( )
A.4 B.5 C.6 D.7
1.设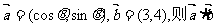 的最小值是 ( )
的最小值是 ( )
A.-3 B.-4 C.-5 D.0
(17)(本小题满分l2分)
已知集合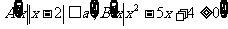 ,若
,若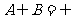 ,求实数
,求实数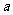 的取值范围.
的取值范围.
(18)(本小题满分12分)
已知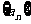 是公比为q的等比数列,且
是公比为q的等比数列,且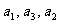 成等差数列.
成等差数列.
(I)求q的值;
(Ⅱ)设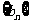 是以2为首项,q为公差的等差数列,其前n项和为
是以2为首项,q为公差的等差数列,其前n项和为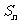 .当
.当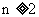 时,比较
时,比较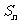 与
与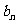 的大小,并说明理由.
的大小,并说明理由.
(19)(本小题满分l2分)
设锐角三角形ABC的内角A,B,C的对边分别为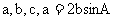 .
.
(I)求B的大小;
(Ⅱ)求 的取值范围.
的取值范围.
(20)(本小题满分l2分)
数列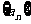 的前n项和为
的前n项和为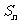 ,
,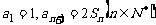
(I)求数列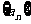 的通项
的通项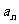 ;
;
(Ⅱ)求数列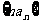 的前n项和Tn
的前n项和Tn
(21)(本小题满分l2分)
某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司交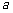 元(3≤
元(3≤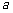 ≤5)的管理费,预计当每件产品的售价为x元(9≤
≤5)的管理费,预计当每件产品的售价为x元(9≤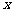 ≤11)时,一年的销售量为
≤11)时,一年的销售量为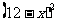 万件.
万件.
(1)求分公司一年的利润L(万元)与每件产品的售价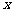 的函数关系式;
的函数关系式;
(2)当每件产品的售价为多少元时,分公司一年的利润L最大,并求出L的最大值Q(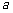 )
)
(22)(本小题满分14分)
设函数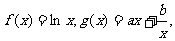 函数
函数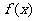 的图像与
的图像与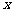 轴的交点也在函数
轴的交点也在函数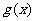 的图像上,且在此点有公切线.
的图像上,且在此点有公切线.
(I)求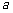 ,b的值;
,b的值;
(Ⅱ)对任意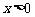 ,试比较
,试比较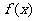 与
与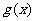 的大小。
的大小。
(13)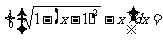 __________.
__________.
(14)在△ABC中,若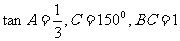 ,则AB=_______________。
,则AB=_______________。
(15)函数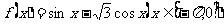 的单调递增区间是___________。
的单调递增区间是___________。
(16)给出以下命题:
①若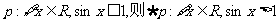 ;
;
②若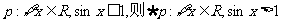 ;
;
③对于函数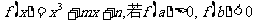 ,则函数
,则函数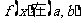 内至 多有一个零点;
内至 多有一个零点;
④对于函数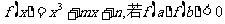 ,则函数
,则函数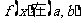 内至多有一个零点,
内至多有一个零点,
其中正确命题的序号是___________(注:把你认为正确的命题的序号都填上).
(1)如果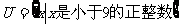 ,A={1,2,3,4},B={3,4,5,6},那么
,A={1,2,3,4},B={3,4,5,6},那么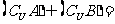
(A){1,2} (B){3,4} (C){5,6} (D){7,8}
(2)已知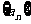 是等差数列,
是等差数列,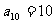 ,其前10项和
,其前10项和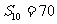 ,则其公差d=
,则其公差d=
(A)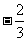 (B)
(B) 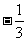 (C)
(C) 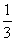 (D)
(D) 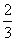
(3)若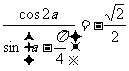 ,则
,则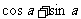 的值为
的值为
(A)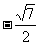 (B)
(B) 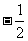 (C)
(C) 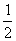 (D)
(D) 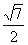
(4)幂函数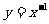 及直线
及直线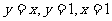 将平面直角坐标系的第一象限分成八个“卦限”:①,②,③,④,⑤,⑥,⑦,⑧(如图所示),那么幂函数
将平面直角坐标系的第一象限分成八个“卦限”:①,②,③,④,⑤,⑥,⑦,⑧(如图所示),那么幂函数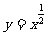 的图象经过的“卦限”是
的图象经过的“卦限”是
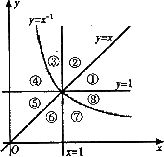
(A)④,⑦ (B)④,⑧ (C)③,⑧ (D)①,⑤
(5)已知函数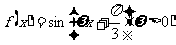 的最小正周期为
的最小正周期为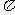 ,则该函数的图象.
,则该函数的图象.
(A)关于点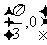 对称 (B)关于直线
对称 (B)关于直线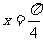 对称
对称
(C)关于点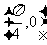 对称 (D)关于直线
对称 (D)关于直线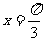 对称
对称
(6)若数列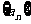 满足
满足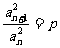 (
(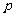 为正常数;
为正常数;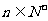 ),则称
),则称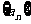 为“等方比数列”.
为“等方比数列”.
甲:数列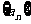 是等方比数列; 乙:数列
是等方比数列; 乙:数列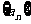 是等比数列,则
是等比数列,则
(A)甲是乙的充分条件但不是必要条件
(B)甲是乙的必要条件但不是充分条件
(C)甲是乙的充要条件
(D)甲既不是乙的充分条件也不是乙的必要条件
(7)函数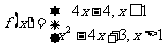 的图象和函数
的图象和函数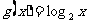 的图象的交点个数是
的图象的交点个数是
(A)4 (B)3 (C)2 (D)1
(8)给出下列四个等式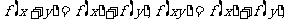
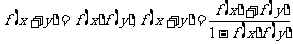 ,下列函数中不满足其中任何一个等式的是
,下列函数中不满足其中任何一个等式的是
(A)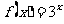 (B)
(B) 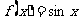 (C)
(C) 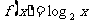 (D)
(D) 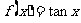
(9)曲线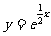 在点
在点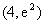 处的切线与坐标轴所围三角形的面积为
处的切线与坐标轴所围三角形的面积为
(A)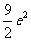 (B)
(B) 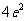 (C)
(C)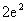 (D)
(D)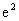
(10)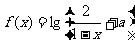 是奇函数,则使
是奇函数,则使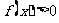 的x的取值范围是
的x的取值范围是
(A)(一1,0) (B)(0,1) (C)(一∞,0) (D)(一∞,0)U(1,+∞)
(11)若不等式组 表示的平面区域是一个三角形区域,则a的取值范围是
表示的平面区域是一个三角形区域,则a的取值范围是
(A)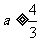 (B)
(B)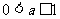 (C)
(C) 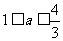 (D)
(D) 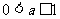 或
或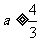
(12)已知二次函数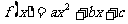 的导数为
的导数为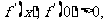 对于任意实数
对于任意实数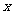 ,有
,有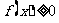 ,则
,则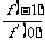 的最小值为
的最小值为
(A)3 (B)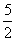 (C)2 (D)0
(C)2 (D)0
第Ⅱ卷(共90分)
(17)(本小题满分l2分)
已知集合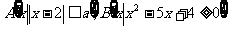 ,若
,若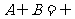 ,求实数
,求实数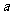 的取值范围.
的取值范围.
(18)(本小题满分12分)
已知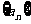 是公比为q的等比数列,且
是公比为q的等比数列,且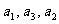 成等差数列.
成等差数列.
(I)求q的值;
(Ⅱ)设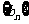 是以2为首项,q为公差的等差数列,其前n项和为
是以2为首项,q为公差的等差数列,其前n项和为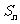 .当
.当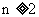 时,比较
时,比较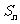 与
与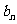 的大小,并说明理由.
的大小,并说明理由.
(19)(本小题满分l2分)
已知函数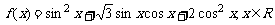
(I)求函数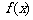 的最小正周期和单调减区间;
的最小正周期和单调减区间;
(Ⅱ)函数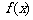 的图象可以由函数
的图象可以由函数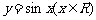 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
(20)(本小题满分l2分)
数列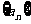 的前n项和为
的前n项和为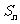 ,
,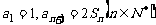
(I)求数列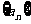 的通项
的通项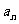 ;
;
(Ⅱ)求数列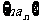 的前n项和Tn
的前n项和Tn
(21)(本小题满分l2分)
某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司交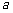 元(3≤
元(3≤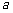 ≤5)的管理费,预计当每件产品的售价为x元(9≤
≤5)的管理费,预计当每件产品的售价为x元(9≤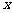 ≤11)时,一年的销售量为
≤11)时,一年的销售量为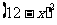 万件.
万件.
(1)求分公司一年的利润L(万元)与每件产品的售价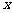 的函数关系式;
的函数关系式;
(2)当每件产品的售价为多少元时,分公司一年的利润L最大,并求出L的最大值Q(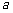 )
)
(22)(本小题满分14分)
设函数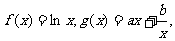 函数
函数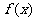 的图像与
的图像与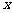 轴的交点也在函数
轴的交点也在函数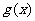 的图像上,且在此点有公切线.
的图像上,且在此点有公切线.
(I)求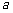 ,b的值;
,b的值;
(Ⅱ)证明:当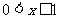 时,
时,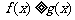 ;当
;当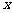 >1时
>1时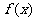 <
<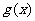 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com