
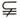 1.设集合
1.设集合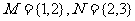 ,集合P (M∪N),则P的个数是 ( )
,集合P (M∪N),则P的个数是 ( )
A.6 B.8 C.7 D.5
2.已知函数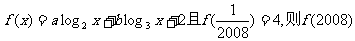 的值为 ( )
的值为 ( )
A.-4 B.2 C.0 D.-2
22.(本小题满分12分)
已知在函数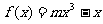 的图象上以N(1,n)为切点的切线的倾斜角为
的图象上以N(1,n)为切点的切线的倾斜角为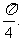
(1)求m、n的值;
(2)是否存在最小的正整数k,使得不等式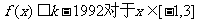 恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
(3)求证: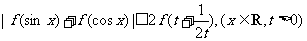
21.(本小题满分12分)
在数列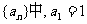 ,其前n项的和Sn满足关系式
,其前n项的和Sn满足关系式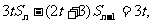
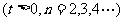 。
。
(1)求证:数列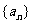 是等比数列;
是等比数列;
(2)求数列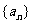 的公比为
的公比为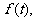 作数列
作数列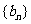 ,使
,使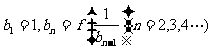 求bn。
求bn。
(3)求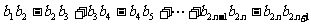 的值。
的值。
20.(本小题满分12分)
在平面直角坐标系内有两个定点F1、F2和动点P,F1、F2的坐标分别为F1(-1,0),F2(1,0),动点P满足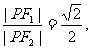 动点P的轨迹为曲线C,曲线C关于直线y=x的对称曲线为曲线C′,直线
动点P的轨迹为曲线C,曲线C关于直线y=x的对称曲线为曲线C′,直线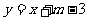 与曲线C′交于A、B两点,O是C′的对称中心,△ABO的面积为
与曲线C′交于A、B两点,O是C′的对称中心,△ABO的面积为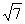 。
。
(1)求曲线C的方程;
(2)求m的值。
19.(本小题满分12分)
如图,矩形ABCD,|AB|=1,|BC|=a,PA⊥平面ABCD,|PA|=1。
(1)BC边上是否存在点Q,使得PQ⊥QD,并说明理由;
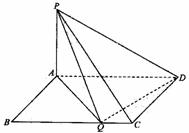 (2)若BC边上存在唯一的点Q使得PQ⊥QD,
(2)若BC边上存在唯一的点Q使得PQ⊥QD,
指出点Q的位置,并求出此时AD与平面
PDQ所成的角的正弦值;
(3)在(2)的条件下,求二面角
Q-PD-A的正弦值。
|
已知a=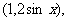 b=
b=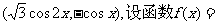 a·b。
a·b。
(1)若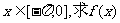 的最大值、最小值并求出对应的x值。
的最大值、最小值并求出对应的x值。
(2)求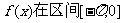 上的递减区间。
上的递减区间。
18.(本小题满分12分)
有A,B,C,D四个城市,它们各自有一个著名的旅游点,依次记为a,b,c,d,把A,B,C,D和a,b,c,d分别写成左、右两列。现在一名旅游爱好者随机用4条城市与旅游点全部连接起来,构成“一一对应”。已知连对的得2分,连错的得0分。
(1)求该爱好者得分的分布列;
(2)求所得分数的数学期望。
16.等差数列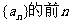 项和为
项和为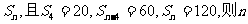 =
。
=
。
15.把一个函数的图象按向量a=(3,-2)平移,得到的图像的解析式为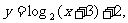 则原来的函数的解析式为
。
则原来的函数的解析式为
。
14.设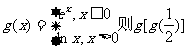 。
。
13.在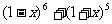 的展开式中,含
的展开式中,含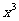 的项的系数是
。
的项的系数是
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com