
21.已知F1、F2分别是椭圆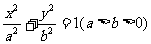 的左、右焦点,其左准线与x轴相交于点N,并且满足
的左、右焦点,其左准线与x轴相交于点N,并且满足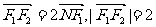 .设A、B是上半椭圆上满足
.设A、B是上半椭圆上满足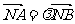 的两点,其中
的两点,其中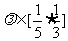 .
.
(I)求此椭圆的方程及直线AB的斜率的取值范围;
(II)过A、B两点分别作此椭圆的切线,两切线相交于一点P,求证:点P在一条定直线上,并求点P的纵坐标的取值范围.
20.某出版社新出版一本高考复习用书,该书的成本为5元/本,经销过程中每本书需付给代理商m元(1≤m≤3)的劳务费,经出版社研究决定,新书投放市场后定价为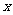 元/本(9≤
元/本(9≤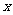 ≤11),预计一年的销售量为
≤11),预计一年的销售量为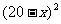 万本.
万本.
(Ⅰ)求该出版社一年的利润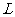 (万元)与每本书的定价
(万元)与每本书的定价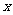 的函数关系式;
的函数关系式;
(Ⅱ)当每本书的定价为多少元时,该出版社一年的利润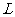 最大,并求出
最大,并求出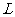 的最大值
的最大值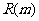
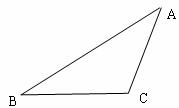
19.如图,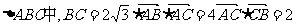 ,双曲线M是以B、C为焦点且过A点.
,双曲线M是以B、C为焦点且过A点.
(I)建立适当的坐标系,求双曲线M的方程;
(II)设过点E(1,0)的直线l分别与双曲线M的左、右支交于F、G两点,直线l的斜率为k,求k的取值范围.
18.已知单调递增等比数列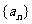 满足
满足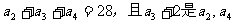 的等差中项.
的等差中项.
(I)求数列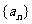 的通项公式;
的通项公式;
(II)若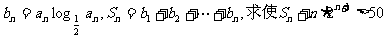 成立的正整数n的最小值.
成立的正整数n的最小值.
17.在锐角三角形ABC中,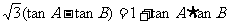 .
.
(I)若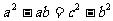 ,求A、B、C的大小;
,求A、B、C的大小;
(II)已知向量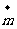 =(sinA,cosA),
=(sinA,cosA),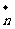 =(cosB,sinB),求
=(cosB,sinB),求 的取值范围.
的取值范围.
16.按下列程序框图运算:
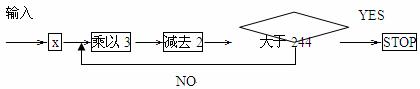
规定:程序运行到“判断结果是否大于244”为1次运算.
若x=5,则运算进行 次才停止;若运算进行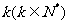 次才停止,则x的取值范围是
次才停止,则x的取值范围是
|
15.定义在R上的函数f(x)满足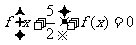 ,且函数
,且函数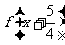 为奇函数.
为奇函数.
给出下列结论:
①函数f(x)的最小正周期是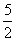 ;
②函数f(x)的图像关于点
;
②函数f(x)的图像关于点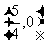 对称;
对称;
③函数f(x)的图像关于直线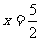 对称; ④函数f(x)的最大值为
对称; ④函数f(x)的最大值为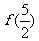 .
.
其中正确结论的序号是 .(写出所有你认为正确的结论的序号)
14.函数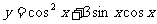 的最小正周期T=
.
的最小正周期T=
.
13.在数列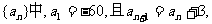 则这个数列的前30项的绝对值之和为
则这个数列的前30项的绝对值之和为
12.点O为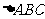 内一点,且存在正数
内一点,且存在正数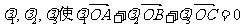 ,设
,设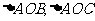 的面积分别为
的面积分别为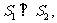 则
则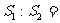 ( )
( )
A.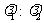 B.
B. 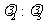 C.
C. 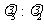 D.
D. 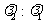
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com