6．某商场有四类食品，其中粮食类、植物油类、动物性食品类及果蔬类分别为40种、10种、30种、20种，现从中抽取一个容量为20的样本进行食品安全检测.若采用分层抽样的方法抽取样本，则抽取的植物油类与果蔬类食品种数之和是　　 　 (　　 )

　　　 A．4　　　　　　　　　　　　 B．5　　　　　　　　　　　　 C．6　　　　　　　　　　　　 D．7

5．已知曲线的一条切线的斜率为，则切点的横坐标为　　　　　　　　　　　　　 (　　 )

　　　 A．1　　　　　　　　　　　　 B．2　　　　　　　　　　　　 C．3　　　　　　　　　　　　 D．4

4．设，则的值域是　　　　　　　　　 　　　　　　　　　　　　　　　　 (　　 )

　　　 A．　　　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　　　　　　　　　　　　 D．

3．设函数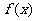是定义在R上的以5为周期的可导偶函数，则曲线处的切线的斜率　　　　　　　 　　　　　　　　　　　　　　　　 (　　 )

　　　 A．－　　　　　　　　　 B．0　　　　　　　　　　　　 C．　　　　　　　　　　　 D．5

2．命题：“若”的逆否命题是　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．若　　　　　　　 B．若

　　　 C．若　　　　　　　 D．若

1．设P和Q是两个集合，定义集合，

　 等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．　　 B．　　 C．　　 D．

6．试确定所有同时满足

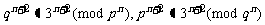
的三无数组(p,q,n),其中p,q为奇素数，n为大于1的整数。

5.求具有如下性质的最小正整数n，将正n边形的每一个顶点任意染上红，黄，蓝三种颜色之一，那么这n个顶点中一定存在四个同色点，它们是一个等腰梯形的顶点(两条边平行，另两条边不平行且相等的凸四边形称为等腰梯形)。

4．设A是正整数集的无限子集，是给定的整数，已知：对任意一个不整除n的素数p，集合A中均有无穷多个元素不被P整除

证明：对任意整数m>1,(m,n)=1，集合A中均存在有限个互不相同的元素，其和S满足S≡1(modm),且S≡0(modn)

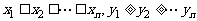3．给定正整数，及实数，满足

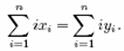
证明：对任意实数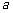，有

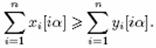
这里[]表示不超过实数的最大整数。

2008年中国数学奥林匹克

(第二十三届全国中学生数学冬令营)

第二天

哈尔滨　 1月20日　 上午8：00~12：30　 每题21分