
8.定义在R上的奇函数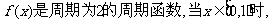
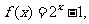
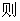
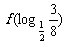 的值为 ( )
的值为 ( )
A.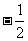 B.
B.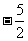 C.-5 D.-6
C.-5 D.-6
7.已知随机变量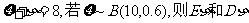 分别为 ( )
分别为 ( )
A.6和2.4 B.2和2.4 C.2和5.6 D.6和6.6
6.已知相交直线l、m都在平面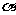 内,并且都不在平面
内,并且都不在平面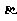 内,若p:l、m中至少有一条与平面
内,若p:l、m中至少有一条与平面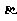 相交;q:平面
相交;q:平面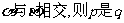 的 ( )
的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.已知向量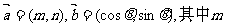 、n、
、n、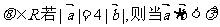 恒成立时,实数
恒成立时,实数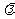 的取值范围是 ( )
的取值范围是 ( )
A.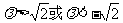 B.
B.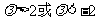
C.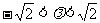 D.
D.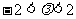
4.直线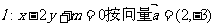 平移后得到的直线
平移后得到的直线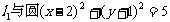 相切,则m的值为 ( )
相切,则m的值为 ( )
A.9或-1 B.5或-5 C.-7或7 D.3或13
3.集合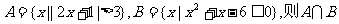 = ( )
= ( )
A.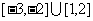 B.
B.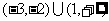
C. D.
D.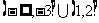
2.函数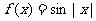 的一个单调递减区间为 ( )
的一个单调递减区间为 ( )
A.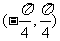 B.
B.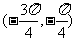 C.
C.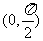 D.
D.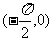
1.复数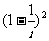 的值为 ( )
的值为 ( )
A.2 B.-2 C.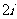 D.-
D.-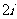
(17)(本小题满分12分)
已知平面内三点A(3,0),B(0,3),C(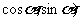 ,O为坐标原点.
,O为坐标原点.
(1)若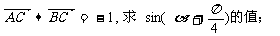
(2)若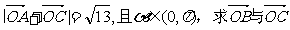 的夹角。
的夹角。
(18)(本小题满分12分)
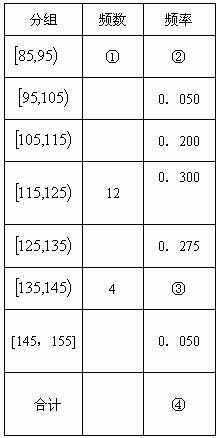
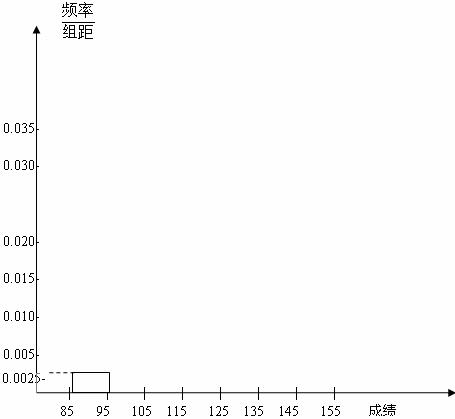
高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
(1)根据图表,①②③④处的数值分别为 ;
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体落在[129,155]中的概率.
(19)(本小题满分12分)
如图,在三棱柱BCE-ADF中,四边形ABCD是正方形,DF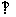 平面ABCD,M、N分别是AB、AC的中点,G是DF上的一点.
平面ABCD,M、N分别是AB、AC的中点,G是DF上的一点.
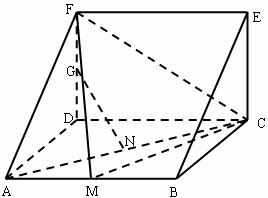
(1)求证: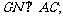
(2)若FG=GD,求证:GA//平面FMC.
20 (本小题共12分)
设椭圆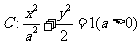 的左右焦点分别为
的左右焦点分别为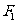 、
、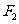 ,
,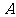 是椭圆
是椭圆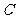 上的一点,且
上的一点,且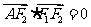 ,坐标原点
,坐标原点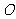 到直线
到直线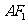 的距离为
的距离为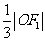 .
.
(Ⅰ)求椭圆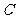 的方程;
的方程;
(Ⅱ)设斜率为1的直线与曲线C交于两点P、Q,求|PQ|的最大值.
(21)(本小题满分12分)
已知函数 的图象经过点M(1,4),曲线在点M处的切线恰好与直线
的图象经过点M(1,4),曲线在点M处的切线恰好与直线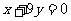 垂直。
垂直。
(Ⅰ)求实数a、b的值;
(Ⅱ)若函数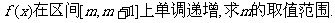
(22)请考生在A、B两题中任选一题做答,如果多做,则按所做第一题记分。作答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑。
(22)A.(本小题满分10分)选修4-1:几何证明选讲
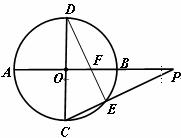
如图所示,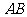 与
与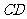 是⊙O的直径,
是⊙O的直径,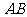
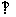
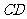 ,
,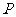 是
是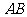 延长线上一点,连
延长线上一点,连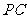 交⊙O于点
交⊙O于点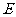 ,连
,连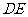 交
交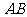 于点
于点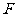 ,若
,若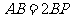 .
.
求证: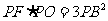
(22)B (本小题满分10分)选修4-2:坐标系与参数方程
在曲线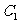 :
: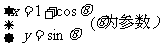 上求一点,使它到直线
上求一点,使它到直线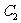 :
:
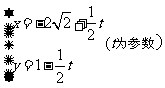 的距离最小,并求出该点坐标和最小距离。
的距离最小,并求出该点坐标和最小距离。
(13)在等差数列{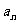 }中,
}中,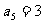 ,前5项的和
,前5项的和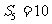 ,则公差d=________.
,则公差d=________.
(14)已知点 表示的平面区域上运动,则
表示的平面区域上运动,则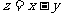 的取值范围是____________ .
的取值范围是____________ .
(15)若命题“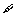 x∈R,使x2+(a-1)x+1<0”是假命题,则实数a的取值范围为
.
x∈R,使x2+(a-1)x+1<0”是假命题,则实数a的取值范围为
.
(16)某小卖部为了了解热茶销售量y(杯)与气温x(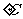 )之间的关系,随机统计了某4天卖出的热茶的杯数与当天气温,并制作了对照表:
)之间的关系,随机统计了某4天卖出的热茶的杯数与当天气温,并制作了对照表:
气温x(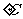 ) ) |
18 |
13 |
10 |
-1 |
|
杯数
y |
24 |
34 |
38 |
64 |
由表中数据算得线性回归方程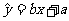 中的
中的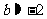 ,预测当气温为
,预测当气温为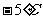 时,热茶销售量为__________杯.(回归系数
时,热茶销售量为__________杯.(回归系数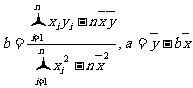 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com