
2.已知 ,且
,且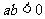 ,则
,则 是复数
是复数 为纯虚数的
为纯虚数的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
1.函数 的定义域是
的定义域是
A.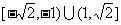 B.
B.
C. D.
D.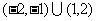
21.(本小题满分14分)
已知函数 定义在区间[一1,1]上,且
定义在区间[一1,1]上,且 ,又P(
,又P( )、Q(
)、Q(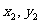 )是其图像上任意两点(
)是其图像上任意两点( ).
).
(1)求证: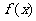 的图像关于点(0,b)成中心对称图形;
的图像关于点(0,b)成中心对称图形;
(2)设直线PQ的斜率为 ,求证:
,求证: <2;
<2;
(3)若0≤ ≤1,求证:
≤1,求证: <1.
<1.
20.(本小题满分13分)
已知向量p//q,其中 ,
, R且
R且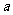 >0,
>0,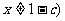 ,把其中
,把其中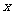 ,
,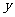 所满足的关系式记为
所满足的关系式记为 ,若函数
,若函数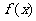 为奇函数,且当
为奇函数,且当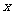 >0时,
>0时,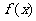 有最小值
有最小值 .
.
(1)求函数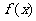 的表达式;
的表达式;
(2)设数列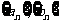 满足如下关系:
满足如下关系: N*),且
N*),且
 ,求数列
,求数列 的通项公式,并求数列
的通项公式,并求数列 N*)前
N*)前 项的和S
项的和S .
.
19.(本小题满分12分)
已知 =(c,o)(c>o),
=(c,o)(c>o), =(
=( ,
, )(
)(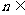 R),
R), 的最小值为1,若动点P同时满足下列三个条件:①
的最小值为1,若动点P同时满足下列三个条件:① ;②
;② ,其中
,其中 R;③动点P的轨迹C经过点B(0,一1).
R;③动点P的轨迹C经过点B(0,一1).
(1)求 的值;
的值;
(2)求曲线C的方程;
(3)是否存在方向向量为 ≠0)的直线
≠0)的直线 ,使
,使 与曲线C交于两个不同的点M、N,且
与曲线C交于两个不同的点M、N,且 ?若存在,求出k的取值范围;若不存在,请说明理由.
?若存在,求出k的取值范围;若不存在,请说明理由.
18.(本小题满分12分)
如图,在直三棱柱ABC-AlBlC1中,AB⊥BC,E是A1C的中点,ED⊥A1C且交AC于D, A1A=AB= BC.
BC.
(1)证明:B1C1//平面A1BC;
(2)证明:A1C⊥平面EDB;
(3)求平面A1AB与平面EDB所成的二面角的大小(仅考虑平面角为锐角的情况).

17.(本小题满分12分)
一个口袋里有5个白球和3个黑球,任意取出一个,如果是黑球,则这个黑球不放回且另外放人一个白球,这样继续下去,直到取出的球是白球为止,求直到取到白球所需的抽取次数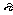 的概率分布及E
的概率分布及E .
.
16.(本小题满分12分)
已知∠A,∠B,∠C是△ABC的三个内角,若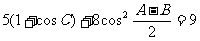 .
.
(1)求证: ;
;
(2)求 的最大值,并求此时∠A、∠B的正切值.
的最大值,并求此时∠A、∠B的正切值.
15.在△ABC中,已知B(一2,0),C(2,0),A(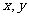 ),给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
),给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
|
条件 |
方程 |
|
①△ABC的周长为10 |
C1:y2=25 |
|
②△ABC面积为10 |
C2: |
|
③在△ABC中,∠A=90° |
C3: |
则满足条件①、②、③的轨迹方程分别为 .(用代号C1、C2、C3填入)
14.为了了解“预防禽流感疫苗”的使用情况,黄冈市卫生部门对本地区9月份至11月份使用疫苗的所有养鸡场进行了调查,根据图和下表提供的信息,可以得出这三个月本地区每月注射了疫苗的鸡的数量平均为 万只.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com