
5.某人为了观看2008年奥运会,从2001年起,每年5月10日到银行存入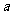 元定期储蓄,若年利率为
元定期储蓄,若年利率为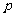 且保持不变,并约定每年到期存款均自动转为新的一年定期,到2008年将所有的存款及利息全部取回(2008年不再存),则可取回的钱的总数(元)为(不计利息税)
且保持不变,并约定每年到期存款均自动转为新的一年定期,到2008年将所有的存款及利息全部取回(2008年不再存),则可取回的钱的总数(元)为(不计利息税)
A.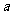 (1+
(1+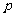 )7 B.
)7 B.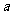 (1+
(1+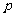 )8
)8
C. [(1+
[(1+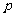 )7一(1+
)7一(1+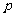 )] D.
)] D. [(1+
[(1+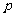 )8一(1+
)8一(1+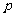 )]
)]
4.函数 ,
, 的增区间是
的增区间是
A.[0, ] B.[
] B.[ ,
, ] C.[
] C.[ ,
, ] D.[
] D.[ ,
, ]
]
3.若
 =9,则实数
=9,则实数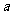 等于
等于
A. B.
B.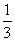 C.一
C.一 D.一
D.一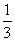
2.若复数 满足对应关系
满足对应关系 ,则
,则 =
=
A.1+i B.一1+i C.2 D.0
1.设集合A={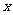 |一1<
|一1<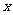 <4,且
<4,且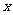 ∈N},B={
∈N},B={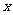 |
| <1},则A
<1},则A B=
B=
A.{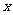 |0<
|0<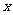 <2}
B.{
<2}
B.{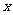 |-1<
|-1<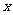 <2} C.{0,1} D.{1}
<2} C.{0,1} D.{1}
21.(本小题满分14分)
已知函数 .
.
(1)求 在[0,1]上的极值;
在[0,1]上的极值;
(2)若对任意 ∈[
∈[ ],不等式
],不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)若关于 的方程
的方程 在[0,1]上恰有两个不同的实根,求实数
在[0,1]上恰有两个不同的实根,求实数 的取值范围.
的取值范围.
20.(本小题满分13分)
已知椭圆 内一定点M(m,0)(m≠0)和直线
内一定点M(m,0)(m≠0)和直线 :
: ,直线
,直线 与
与 轴交点为K.
轴交点为K.
(1)过M的任意直线与椭圆交于A、B两点,证明:∠AKM=∠BKM;
(2)过点K的直线与椭圆相交于A、E两点,设 ,过点E且平行于直线
,过点E且平行于直线 的直线与椭圆相交于另一点B,证明:
的直线与椭圆相交于另一点B,证明: .
.
19.(本小题满分12分)
如图,在直三棱柱ABC-A1B1Cl中,∠ACB=90°,CB=1,CA= ,AA1=
,AA1= ,M是侧棱CC1上一点,AM⊥BA1.
,M是侧棱CC1上一点,AM⊥BA1.
(1)求证:AM⊥平面A1BC;
(2)求二面角B-AM-C的大小;
(3)求点C到平面ABM的距离.

18.(本小题满分12分)
过点P(1,0)作曲线C: 的切线,切点为Q1,设Q1在
的切线,切点为Q1,设Q1在 轴上的投影是Pl,又过P1作曲线C的切线,切点为Q2,设Q2在
轴上的投影是Pl,又过P1作曲线C的切线,切点为Q2,设Q2在 轴上的投影是P2,……依次下去,得到一系列Q1、Q2、…、Q
轴上的投影是P2,……依次下去,得到一系列Q1、Q2、…、Q ,设点Q
,设点Q 横坐标为
横坐标为 .
.
(1)求 的值,并求出
的值,并求出 与
与 的关系;
的关系;
(2)令 ,设数列{
,设数列{ }的前
}的前 项和为
项和为 ,求
,求
17.(本小题满分12分)
一次小测验共有3道选择题和2道填空题,每答对1道题得20分,答错或不答得0分;某同学 答对每道选择题的概率是0.8,答对每道填空题的概率是0.5,各道题答对与否互不影响.
(1)求该同学恰好答对2道选择题和1道填空题的概率;
(2)求该同学至多答对4道题的概率;
(3)若该同学已经答对了2道填空题,把他这次测验的得分记为 ,求
,求 的概率分布列及数学期望.
的概率分布列及数学期望.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com