
6.袋子中有5个球(3个白色、2个黑色),现每次取一个,无放回地抽取两次,则在第一次抽到白球的条件下,第二次抽到白球的概率为( )
A.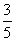 B.
B.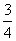 C.
C.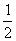 D.
D.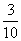
5.设随机变量X的分布列为P(X=i)=a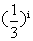 ,i=1,2,3,则a的值为( )
,i=1,2,3,则a的值为( )
A.1 B.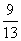 C.
C.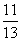 D.
D.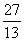
4.椭圆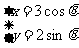 (θ为参数)的焦距为(
)
(θ为参数)的焦距为(
)
A.2 B.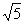 C.2
C.2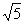 D.2
D.2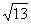
3.在极坐标第中,过点(2,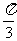 ),并且和极轴垂直的直线的极坐标方程为( )
),并且和极轴垂直的直线的极坐标方程为( )
A.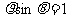 B.
B.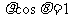 C.
C.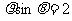 D.
D.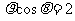
2.设随机变量n等可能地取值1,2,3,4,5,6,7,8,又设随机变量X=2n+1,则P(X<6)的值为( )
A.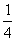 B.
B.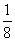 C.
C.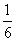 D.
D.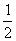
1.若直线的参数方程为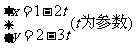 ,则直线的斜率为( )
,则直线的斜率为( )
A.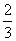 B.-
B.-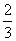 C.
C.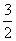 D.-
D.-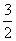
22.(本题满分14分)
已知函数f(x)=ax2一x+2a一1(a为正常数).
(1)设f(x)在区间[1,2]上的最小值为g(a),求g(a)的表达式;
(2)设h(x)=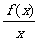 ,若函数h(x)在区间[1,2]上是增函数,求实数a的取值范围。
,若函数h(x)在区间[1,2]上是增函数,求实数a的取值范围。
21.(本题满分12分)设a∈R,函数f(x)=ex+a·e-x的导函数是f’(x),且f’(x)是奇函数.
(I)求a的值;
(2)证明:y=f(x)在(0,+∞)上单调递增;
(3)若曲线y=f(x)的一条切线的斜率是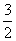 ,求切点的横坐标.
,求切点的横坐标.
(参考公式:(e-x)’=-e-x)
20.(本题满分12分)已知幂函数f(x)=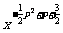 (p∈z)在(0,+∞)上是增函数,且在其定义域内是偶函数.
(p∈z)在(0,+∞)上是增函数,且在其定义域内是偶函数.
(1)求P的值,并写出相应的函数f(x)
(2)对于(1)中求得的函数f(x),设函数g(x)=(2q-1)f(x)+x+1,问是否存在实数q使得g(x)在区间(一∞,一4]上是减函数,且在(一4,0)上是增函数?若存在,请求出q来;若不存在,请说明理由.
19.(本题满分12分)某工厂生产某种零件,每个零件的成本为40元,出厂单价为60元.该厂为鼓励销售商订购,决定:当一次订购量超过100个时,每多订购1个,订购的全部零件的出厂单价就降价0.02元,但实际出厂单价不能低于51元.
(1)当一次订购量为多少时,零件的实际出厂单价恰降为51元?
(2)设一次订购量为x个,销售的利润为P元,写出函数P=f(x)的表达式.(工厂售出一个零件的利润=实际出厂单价一成本)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com