
2.函数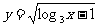 的定义域是( )
的定义域是( )
A.(3,+∞) B.(4,+∞) C.[3,+∞) D.[4,+∞)
1.设全集U={1,3,5,7},集合A={3,5},B={1,3,7},则A∩(CUB)等于( )
A.{5} B.{3,5} C.{1,5,7} D.
21.(本小题满分13分)设函数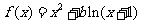 .
.
①若对定义域内任意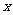 ,都有
,都有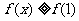 成立,求实数
成立,求实数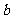 的值
的值
②若函数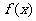 在定义域上是单调函数,求
在定义域上是单调函数,求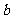 的范围;
的范围;
③若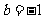 ,证明对任意正整数
,证明对任意正整数 ,不等式
,不等式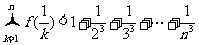 都成立.
都成立.
20.(本小题满分13分)设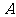 、
、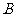 分别为双曲线
分别为双曲线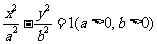 的左右顶点,双曲线的实轴长为
的左右顶点,双曲线的实轴长为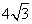 ,焦点到渐近线的距离为
,焦点到渐近线的距离为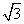 .
.
(1)求双曲线的方程;
(2)已知直线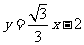 与双曲线的右支交于
与双曲线的右支交于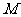 、
、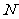 两点,且在双曲线的右支上存在点
两点,且在双曲线的右支上存在点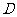 ,使
,使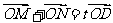 ,求
,求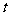 的值及点
的值及点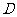 的坐标.
的坐标.
19.(本小题满分13分)已知等差数列 的首项为
的首项为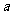 ,公差为
,公差为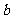 ,且不等式
,且不等式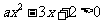 的解集为
的解集为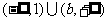 .
.
(1)求数列 的通项公式及前
的通项公式及前 项和
项和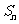 ;
;
(2)若数列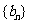 满足
满足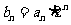 ,求数列
,求数列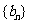 的前
的前 项和
项和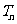 .
.
18.(本题满分12分)某班10名同学在一次测试中英语和法语成绩(单位:分)如下图所示:
|
法语 |
75 |
69 |
58 |
58 |
46 |
51 |
32 |
50 |
53 |
78 |
|
英语 |
52 |
58 |
68 |
77 |
38 |
85 |
43 |
44 |
60 |
65 |
(1)比较哪门课程的平均成绩更高;
(2)计算10名同学法语成绩的样本方差;
(3)计算两门功课成绩相差不超过10分的概率.
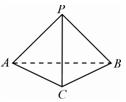
17.(本题满分12分)在三棱锥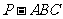 中,
中,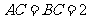 ,
,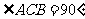 ,
,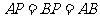 ,
,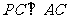
(1)求证: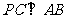 ;
;
(2)求二面角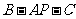 的余弦值;
的余弦值;
(3)求点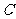 至平面
至平面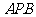 的距离.
的距离.
16.(本小题满分12分)在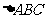 中,
中,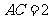 ,
,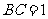 ,
,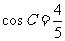 .
.
(1)求边 的长; (2)求
的长; (2)求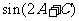 的值.
的值.
15.我们称离心率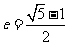 的椭圆叫做“黄金椭圆”,若
的椭圆叫做“黄金椭圆”,若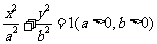 为黄金椭圆,以下四个命题:
为黄金椭圆,以下四个命题:
(1)长半轴长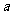 ,短半轴长
,短半轴长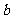 ,半焦距
,半焦距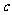 成等比数列.
成等比数列.
(2)一个长轴顶点与其不同侧的焦点以及一个短轴顶点构成直角三角形.
(3)以两条通经的4个端点为顶点的四边形为正方形.
(4) 、
、 为椭圆上任意两点,
为椭圆上任意两点,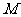 为
为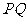 中点,只要
中点,只要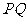 与
与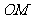 的斜率存在,必有
的斜率存在,必有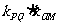 的定值.
的定值.
其中正确命题的序号为 .
14.设点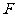 为
为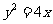 的焦点,
的焦点,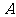 、
、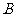 、
、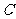 为该抛物线上三点,若
为该抛物线上三点,若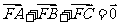 ,则
,则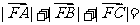 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com