
19.(本小题满分12分)设函数 是
是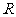 上的奇函数.
上的奇函数.
(1)求 的值;
的值;
(2)对任意给定的正数 ,解不等式
,解不等式 .
.
18.(本小题满分12分)已知 分别为△
分别为△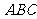 内角
内角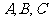 的对边,
的对边, ,
, ,且
,且 .
.
(1)求角A的大小;
(2)若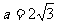 ,三角形的面积为
,三角形的面积为 ,求
,求 的值.
的值.
17.(本小题满分12分)设函数 和
和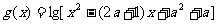 的定义域分别为集合A和B.若
的定义域分别为集合A和B.若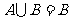 ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.
16.在△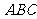 中,
中, 为中线
为中线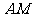 上一动点,若
上一动点,若 ,则
,则 的最小值是____.
的最小值是____.
15.若函数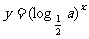 (
( ,且
,且 )在
)在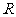 上为减函数,则
上为减函数,则 ____.
____.
14.若数列 满足:
满足: ,且
,且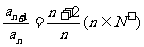 ,则当
,则当 时,
时, ____.
____.
13.若 ,
, ,且点
,且点 满足
满足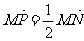 ,
, 为坐标原点,则
为坐标原点,则 ____.
____.
12.若△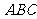 内接于半径为1的⊙
内接于半径为1的⊙ ,且
,且 ,设
,设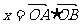 ,
, ,
,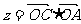 ,则
,则
A. ,△
,△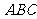 的面积为
的面积为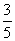 B.
B. ,△
,△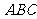 的面积为
的面积为
C. ,△
,△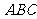 的面积为
的面积为 D.
D. ,△
,△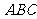 的面积为
的面积为
第II卷(非选择题 共90分)
11.若非零向量 与
与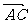 满足:
满足: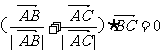 ,且
,且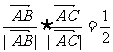 ,则△
,则△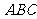 是
是
A.三边均不相等的三角形 B.直角三角形
C.等腰非等边三角形 D.等边三角形
10.在等比数列 中,
中, ,公比
,公比 ,设其前
,设其前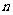 项的积为
项的积为 ,即
,即 ,则
,则 中的最大值是
中的最大值是
A.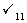 B.
B.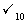 C.
C.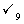 D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com