
6.设函数f(x)定义在实数集上,它的图象关于直线x=1对称,且当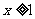 时
时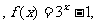 则有 ( )
则有 ( )
A.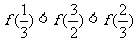 B.
B.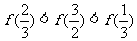
C.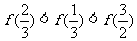 D.
D.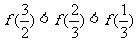
5.同时满足两个条件:①定义域内是减函数 ②定义域内是奇函数的函数是 ( )
A.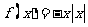 B.
B.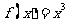 C.
C.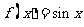 D.
D.
4.等差数列 的前
的前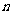 项和为
项和为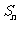 ,且
,且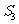 =
=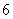 ,
,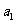 =
=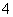 ,则公差
,则公差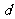 等于 ( )
等于 ( )
A.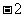 B.
B.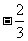 C.
C.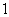 D.
D.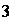
3.函数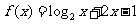 的零点必落在区间 ( )
的零点必落在区间 ( )
A.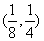 B.
B.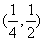 C.
C.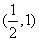 D.
D.
2. 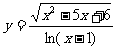 的定义域为 ( )
的定义域为 ( )
A.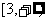 B.
B.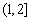 C.
C.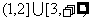 D.
D.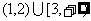
1.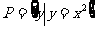 ,
,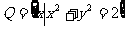 ,则
,则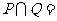 ( )
( )
A.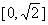 B.
B.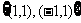 C.
C. D.
D.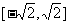
22.(本题满分15分)
对任意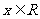 ,给定区间
,给定区间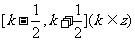 ,设函数
,设函数 表示实数
表示实数 与
与 的给定区间内整数之差的绝对值.
的给定区间内整数之差的绝对值.
|
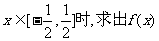 的解析式;当
的解析式;当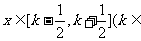 Z)时,写出用绝对值符号表示的
Z)时,写出用绝对值符号表示的 的解析式;
的解析式;
(2)求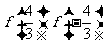 的值,判断函数
的值,判断函数
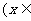 R)的奇偶性,并证明你的结论;
R)的奇偶性,并证明你的结论;
(3)当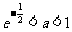 时,求方程
时,求方程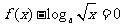 的实根.(要求说明理由,
的实根.(要求说明理由,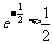 )
)
21.(本题满分15分)
已知 是定义在
是定义在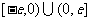 上的奇函数,当
上的奇函数,当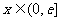 时,
时,
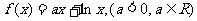
(1)求 的解析式;
的解析式;
(2)是否存在实数a,使得当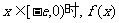 的最小值是3?如果存在,求出a的值;如果不存在,请说明理由。
的最小值是3?如果存在,求出a的值;如果不存在,请说明理由。
20.(本题满分14分)
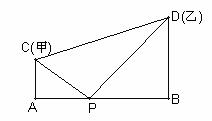
如图,沿河边AB建一水站P供甲、乙两个学校共同使用,已知学校甲离河边1千米,学校乙离河边2千米,而甲、乙两校相距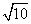 千米,如果两校决定用同一种造价的水管送水.
千米,如果两校决定用同一种造价的水管送水.
(1)设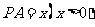 ,试将
,试将 表示成送水需要的水管总长
表示成送水需要的水管总长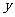 的函数;
的函数;
(2)问水站P建在什么位置,购买水管的费用最低?
19.(本题满分14分)
已知函数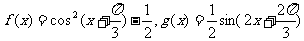
(1)要得到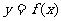 的图像,只需把
的图像,只需把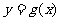 的图像经过怎样的变换?
的图像经过怎样的变换?
(2)设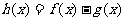 ,求①函数
,求①函数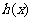 的最大值及对应的
的最大值及对应的 的值;
的值;
②函数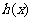 的单调递增区间。
的单调递增区间。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com