
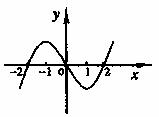
7.设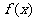 是一个三次函数,
是一个三次函数,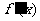 为其导函数,如图所示的是
为其导函数,如图所示的是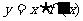 的图象的一部分,则
的图象的一部分,则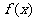 的极大值与极小值分别是
( )
的极大值与极小值分别是
( )
A.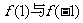 B.
B.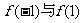 C.
C.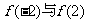 D.
D.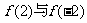
6.顶点在同一球面上的正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=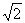 ,则A、C两点间的球面距离是 ( )
,则A、C两点间的球面距离是 ( )
A.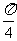 B.
B.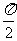 C.
C.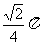 D.
D.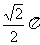
5.要从10名男生和5名女生中选出6人组成啦啦队,若按性别依此比例分层抽样且某男生担任队长,则不同的抽样方法数是 ( )
A.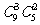 B.
B.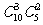 C.
C.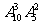 D.
D.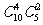
4.已知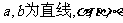 为平面,
为平面,
①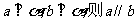 ; ②
; ②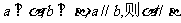 ;
;
③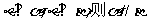 ; ④
; ④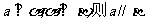 。
。
以上结论正确的是 ( )
A.①② B.①④ C.③④ D.②③
3.已知两个正数a、b的等差中项是5,则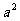 、
、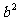 的等比中项的最大值为 ( )
的等比中项的最大值为 ( )
A.100 B.50 C.25 D.10
2.已知向量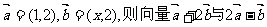 ( )
( )
A.垂直的必要条件是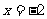 B.垂直的充要条件是
B.垂直的充要条件是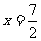
C.平行的充分条件是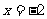 D.平行的充要条件是
D.平行的充要条件是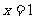
1.已知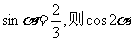 的值是 ( )
的值是 ( )
A.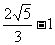 B.
B.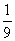 C.
C.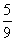 D.
D.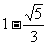
22.(本小题满分12分)
 是抛物线
是抛物线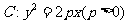 上的两个动点,
上的两个动点, 是焦点,直线
是焦点,直线 不垂直于
不垂直于 轴且交
轴且交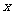 轴于点
轴于点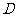 .
.
(1)若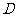 与
与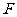 重合,且直线
重合,且直线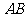 的倾斜角为
的倾斜角为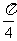 ,求证:
,求证: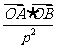 是常数(
是常数(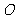 是坐标原点);
是坐标原点);
(2)若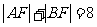 ,线段
,线段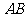 的垂直平分线恒过定点
的垂直平分线恒过定点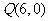 ,求抛物线
,求抛物线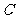 的方程;
的方程;
21.已知函数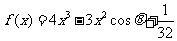 ,其中
,其中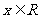 ,
,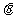 为参数,且0≤
为参数,且0≤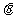 ≤
≤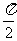 .
.
(1)当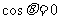 时,判断函数
时,判断函数 是否有极值;
是否有极值;
(2)要使函数 的极小值大于零,求参数
的极小值大于零,求参数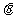 的取值范围;
的取值范围;
(3)若对(2)中所求的取值范围内的任意参数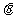 ,函数
,函数 在区间
在区间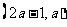 内都是增函数,求实数
内都是增函数,求实数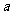 的取值范围。
的取值范围。
20.(本小题满分12分)
已知递增的等比例数列{an}满足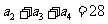 ,且
,且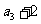 是
是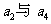 的等差中项.
的等差中项.
(I)求数列{an}的通项公式;
(II)若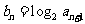 ,Sn是数列
,Sn是数列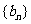 的前n项和,求使
的前n项和,求使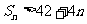 成立的n最小值.
成立的n最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com