
1.定义映射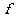 :
: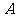 →
→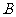 ,若集合
,若集合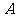 中元素
中元素 在对应法则
在对应法则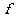 作用下的象为
作用下的象为 ,则
,则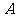 中元素9的象是 ( )
中元素9的象是 ( )
A. 3
B.
3
B. 2 C.2 D.3
2 C.2 D.3
22.(本小题满分12分)
设a∈R,函数 (
(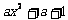 ),其中e是自然对数的底数.
),其中e是自然对数的底数.
(Ⅰ) 判断函数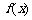 在R上的单调性;
在R上的单调性;
(Ⅱ) 当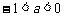 时,求函数
时,求函数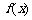 在[1,2]上的最小值.
在[1,2]上的最小值.
21.(本小题满分12分)
已知双曲线 =1(a>0,b>0)的一条渐近线方程为y=
=1(a>0,b>0)的一条渐近线方程为y=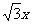 ,两条准线的距离为1.
,两条准线的距离为1.
(Ⅰ)求双曲线的方程;
(Ⅱ)直线l过坐标原点O且和双曲线交于两点M,N,点P为双曲线上异于M,N的一点,且直线PM,PN的斜率均存在,求kPM·kPN的值.
20.(本小题满分12分)
设数列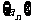 的前
的前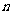 项和为
项和为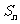 ,且满足
,且满足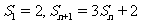
 .
.
(Ⅰ)求证:数列 为等比数列;
为等比数列;
(Ⅱ)设 ,求证:
,求证: .
.
19.(本小题满分12分)
甲、乙两袋装有大小相同的红球和白球,其中甲袋装有1个红球,4个白球;乙袋装有2个红球,3个白球。现从甲.乙两袋中各任取2个球。
(Ⅰ)用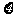 表示取到的4个球中红球的个数,求
表示取到的4个球中红球的个数,求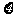 的分布列及
的分布列及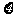 的数学期望;
的数学期望;
(Ⅱ)求取到的4个球中至少有2个红球的概率。
18.(本小题满分12分)
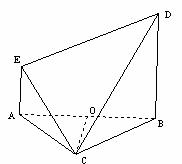
如图,等边 与直角梯形ABDE所在平面垂直,
与直角梯形ABDE所在平面垂直, ,AE⊥AB,
,AE⊥AB,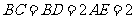 ,O为AB的中点.
,O为AB的中点.
(Ⅰ)证明: ;
;
(Ⅱ)求二面角 的大小.
的大小.
17.(本小题满分10分)
设函数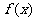 =p·q,其中向量p=
=p·q,其中向量p=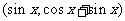 ,q=
,q= x
x R.
R.
(Ⅰ)求函数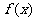 的最大值;
的最大值;
(Ⅱ)求函数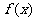 的单调递增区间.
的单调递增区间.
16.若球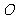 的表面积为
的表面积为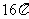 ,边长为2的正三角形
,边长为2的正三角形 的三个顶点在球
的三个顶点在球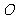 的表面上,则球心
的表面上,则球心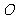 到平面
到平面 的距离为
.
的距离为
.
15.已知实数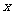 .
.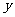 满足
满足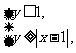 则
则 的最大值是
.
的最大值是
.
14.设F为抛物线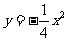 的焦点,与抛物线相切于点
的焦点,与抛物线相切于点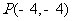 的直线l与x轴的交点为Q,
的直线l与x轴的交点为Q,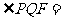 _________________.
_________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com