
5.为得到函数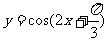 的图象,只需将函数
的图象,只需将函数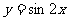 的图象 ( )
的图象 ( )
A.向左平移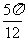 个单位 B.向右平移
个单位 B.向右平移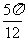 个单位
个单位
C.向左平移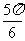 个单位 D.向右平移
个单位 D.向右平移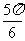 个单位
个单位
4.在(0,2π)内,使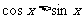 成立的
成立的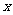 的取值范围为 ( )
的取值范围为 ( )
A.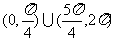 B.
B.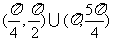
C.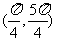 D.
D.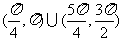
3.若数列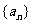 满足:
满足: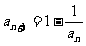 ,
,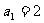 ,则
,则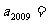 ( )
( )
A.1 B.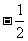 C.
C.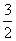 D.
D.
2.设函数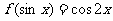 ,则
,则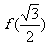 的值为 ( )
的值为 ( )
A. B.
B. C.
C. D.
D.
1.下列各式中值为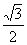 的是 ( )
的是 ( )
A. B.
B.
C.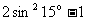 D.
D.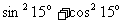
22.已知数列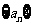 的前n项和为
的前n项和为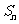 ,对一切正整数n,点
,对一切正整数n,点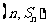 都在函数
都在函数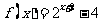 的图像上
的图像上
(1)求数列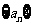 的通项公式;
的通项公式;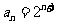
(2)设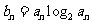 ,求数列
,求数列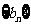 的前n项和
的前n项和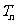 ;错位相减得
;错位相减得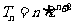
(3)求证: 。
。
21.如下图,某小区准备绿化一块直径为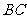 的半圆形空地,
的半圆形空地,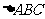 外的地方种草,
外的地方种草,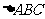 的内接正方形
的内接正方形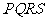 为一水池,其余地方种花.若
为一水池,其余地方种花.若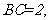
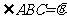 ,设
,设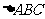 的面积为
的面积为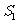 ,正方形
,正方形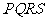 的面积为
的面积为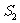 ,将比值
,将比值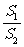 称为“规划合理度”.
称为“规划合理度”.
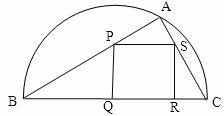
(1)试用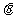 表示
表示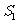 和
和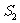 ;
;
(2)求“规划合理度”取得最小值时的角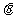 的大小.
的大小.
20.已知函数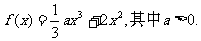
(1)当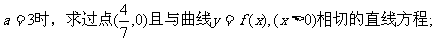
(2)若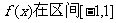 上的最小值为
上的最小值为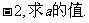
19.某高级中学共有学生2000人,各年级男、女生人数如下表:
|
|
高一 |
高二 |
高三 |
|
女生 |
373 |
x |
y |
|
男生 |
377 |
370 |
z |
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.
(1)现用分层抽样的方法在全校抽取48名学生,问应在高三年级抽取多少人?
(2)已知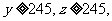 求高三年级女生比男生多的概率.
求高三年级女生比男生多的概率.
18.已知命题p: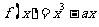 在(2,+∞)为增函数;命题q:
在(2,+∞)为增函数;命题q: 在(1,2)为减函数。若p或q为真,p且q为假,求实数
在(1,2)为减函数。若p或q为真,p且q为假,求实数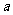 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com