
5.椭圆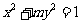 的焦点在
的焦点在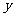 轴上,长轴长是短轴长的两倍,则
轴上,长轴长是短轴长的两倍,则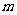 的值为( )
的值为( )
A. B. C.2 D.4
4.若中心在原点,焦点在坐标上的椭圆短轴端点是双曲线y2-x2=1的顶点,且该椭圆的离心率与此双曲线的离心率的乘积为1,则该椭圆的方程为( )
A.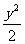 +x2=1 B.
+x2=1 B.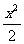 +y2=1 C.
+y2=1 C.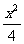 +y2=1 D.
+y2=1 D.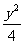 +x2=1
+x2=1
3.“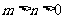 ”是“方程
”是“方程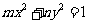 表示焦点在y轴上的椭圆”的( )
表示焦点在y轴上的椭圆”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
2.已知命题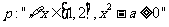 ,命题
,命题 ,若命题“
,若命题“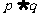 ” 是真命题,则实数
” 是真命题,则实数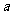 的取值范围是( )
的取值范围是( )
A. B.
B. 或
或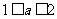
C.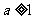 D.
D. 或
或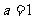
1.命题“存在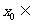 R,
R,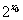
 0”的否定是( )
0”的否定是( )
A.不存在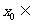 R,
R, 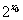 >0 B.存在
>0 B.存在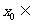 R,
R, 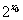
 0
0
C.对任意的 R,
R, 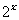
 0
D.对任意的
0
D.对任意的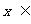 R,
R, 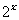 >0
>0
20.(12分)已知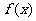 是定义在
是定义在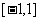 上的奇函数,而且
上的奇函数,而且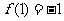 ,若
,若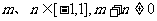 时有
时有 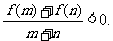
(1)证明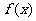 在
在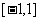 上为减函数;
上为减函数;
(2)解不等式: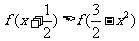 ;
;
(3)若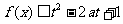 对所有
对所有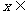
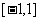 ,
,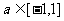 恒成立,求实数
恒成立,求实数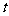 的取值范围.
的取值范围.
19.(12分)已知函数
(1)求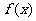 的定义域、值域;
的定义域、值域;
(2)判断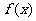 的单调性,并证明.
的单调性,并证明.
18.(9分)若方程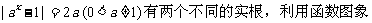 求常数
求常数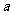 的取值范围.
的取值范围.
17.(9分)用定义判断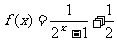 的奇偶性.
的奇偶性.
16.(8分)求函数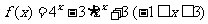 的最小值和最大值.
的最小值和最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com