
6.B.解析: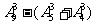 = 420,故选B.
= 420,故选B.
5.A.解析: 圆心O到直线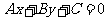 的距离
的距离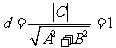 ,所以
,所以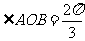 ,,所以
,,所以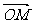 ·
·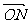 =(·
=(·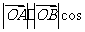
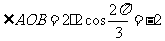 ,故选A.
,故选A.
4.C.解析:前后两组数据波动情况一样,故选C.
3.D.解析: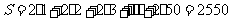 ,故选D.
,故选D.
2.A.解析: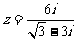 =
= 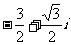 ,故选A.
,故选A.
1.B.解析: A = B =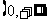 ,故选B.
,故选B.
21.(本小题满分14分)已知A(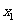 ,
,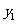 ),B(
),B(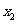 ,
,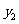 )是函数
)是函数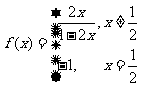 的图象上的任意两点(可以重合),点M在直线
的图象上的任意两点(可以重合),点M在直线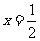 上,且
上,且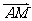 =
=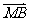 .
.
(Ⅰ)求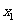 +
+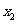 的值及
的值及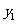 +
+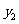 的值;
的值;
(Ⅱ)已知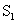 =0,当n≥2时,
=0,当n≥2时,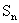 =
=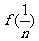 +
+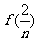 +
+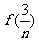 +
+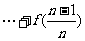 ,求
,求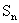 ;
;
(Ⅲ)在(Ⅱ)的条件下,设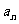 =
=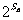 ,
,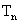 为数列{
为数列{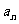 }的前
}的前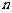 项和,若存在正整数
项和,若存在正整数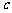 、m,使得不等式
、m,使得不等式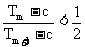 成立,求c和m的值.
成立,求c和m的值.
[答案及详细解析]
20.(本小题满分14分)(本小题满分14分)已知椭圆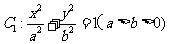 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C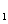 上任一点,MN是圆
上任一点,MN是圆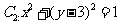 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为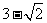 的直线
的直线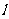 恰好与圆
恰好与圆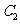 相切.
相切.
(Ⅰ)已知椭圆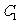 的离心率;
的离心率;
(Ⅱ)若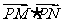 的最大值为49,求椭圆C
的最大值为49,求椭圆C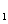 的方程.
的方程.
19.(本小题满分14分)
已知函数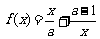 (
(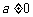 且
且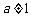 ).
).
(Ⅰ)试就实数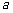 的不同取值,写出该函数的单调递增区间;
的不同取值,写出该函数的单调递增区间;
(Ⅱ)已知当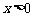 时,函数在
时,函数在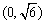 上单调递减,在
上单调递减,在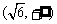 上单调递增,求
上单调递增,求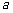 的值并写出函数
的值并写出函数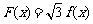 的解析式;
的解析式;
(Ⅲ)记(Ⅱ)中的函数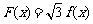 的图像为曲线
的图像为曲线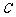 ,试问是否存在经过原点的直线
,试问是否存在经过原点的直线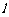 ,使得
,使得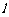 为曲线
为曲线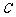 的对称轴?若存在,求出
的对称轴?若存在,求出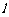 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
18.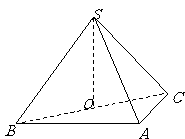 (本小题满分13分)如图,在三棱锥
(本小题满分13分)如图,在三棱锥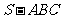 中,侧面
中,侧面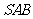 与侧面
与侧面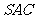 均为等边三角形,
均为等边三角形,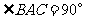 ,
,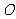 为
为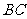 中点.
中点.
(Ⅰ)证明: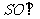 平面
平面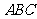 ;
;
(Ⅱ)求二面角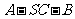 的余弦值.
的余弦值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com