
9.∵P=B,即{1,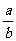 ,b}={0,a+b,b2}
,b}={0,a+b,b2}
注意到b≠0,∴ a=0 ,从而b和b2中有一个为1,由集合中的元素的互异性知b≠1,
∴ b2=-1,从而b=-1,
∴ P={-1,0,1}.
8.2,4
1.D 2.A 3.C 4.B 5.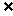 ,∈ 6.A B 7.B
,∈ 6.A B 7.B
10、解:分类讨论:
①A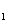 =时,A
=时,A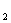 =A,只有一种分拆
=A,只有一种分拆
②A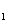 是单元素集时,依题意知有6种
是单元素集时,依题意知有6种
③A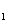 是双元素集合时, A
是双元素集合时, A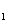 有3种选法
有3种选法
比如A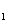 ={a
={a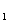 ,a
,a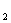 }则A
}则A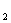 ={a
={a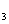 }或{a
}或{a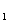 , a
, a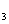 }或{a
}或{a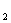 , a
, a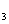 }
}
或{a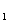 ,a
,a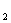 , a
, a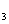 }共4种, 所以共有3×4=12种
}共4种, 所以共有3×4=12种
④A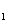 =A时, A
=A时, A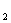 可任意取元素有8种取法,
可任意取元素有8种取法,
综上,共有1+6+12+8=27种不同分拆。
第1章集合 单元检测
9、解:设听数学、历史、音乐讲座的学生分别构成集合A、B、C。
用card(A)_表示听数学讲座的人数,用card(B)表示听历史讲座的人数,用card(C)表示听音乐讲座的人数。则
card(A) =75,card(B)=68, card(C)=61,card(A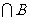 ) =17,card(A
) =17,card(A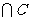 ) =12,card(C
) =12,card(C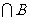 ) =9, card(A
) =9, card(A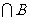
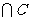 )=6。
)=6。
由于card(A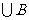
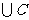 ) = card(A) +card(B)+ card(C)- card(A
) = card(A) +card(B)+ card(C)- card(A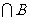 ) -card(A
) -card(A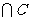 )
)
-card(C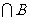 )+ card(A
)+ card(A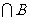
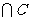 )=75+68+61-17-12-9+6=172(人)
)=75+68+61-17-12-9+6=172(人)
所以听讲座的人数为172人。
1、D 2、C 3、C 4、-1或5 5、A 6、C 7、1 8、9
11.解:分别化简集合A、B得A={1,2},B={1,a-1},
∵ B A
A
∴ a-1≠1且a-1≠2
所以 a-1≠2,3.
第6课 交集、并集
10.解: A={-2,1}
∵A∪B=A,
∴B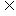 A={-2,1}.
A={-2,1}.
若 m=0,则方程 mx+1=0无解,
∴B=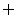 满足B
满足B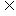 A,
A,
∴m=0符合要求;
若 m≠0,则方程 mx+1=0的解为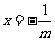 ,
,
∴B={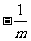 }.由题意知:
}.由题意知:
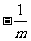 ∈{-2,1}.∴m=0符合要求;
∈{-2,1}.∴m=0符合要求;
∴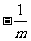 =-2或
=-2或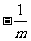 =1,
=1,
∴m=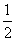 或m=-1,
或m=-1,
故所求m的集合为{-1,0,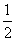 }.
}.
9.解:∵A={-3,2},B=(-3,3),C={1}
∴A∩B={2}
∴(A∩B)∪C={1,2}
8.a≥3,a<3,a≤-4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com