7．B　 A

1．A　　 2．D　　 3．D　　 4．A　　 5．C　　 6．M = P

11．答：(1)是互不相同的集合．

　　　 (2)①{x|y=x²+3x-2}=R，

②{y| y=x²+3x-2}={y|y≥1}

　　　　　　 ③{(x,y)| y=x²++3x-2}={点P是抛物线y=x²+3x-2上的点}

第3课 子集、全集、补集

10．证明：

　　 ∵　 x₁∈A，x₂∈A

　　 ∴设x₁=a₁+b₁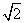，x₂=a₂+b₂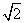

∴x₁x₂=( a₁+b₁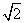)( a₂+b₂)

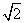=(a₁a₂++2b₁b₂)+(a₁b₂+a₂b₁)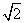∈A

∴　 x₁x₂∈A

9．解： ∵　 5∈A　 ∴ a²+2a-3=5

　即a=2或a=-4

　　　 当a=2时，A={2，3，5}，B=

{2，5}，与题意矛盾；

　　 　　当a=-4时，A={2，3，5}，B={2,1}，

满足题意，　 ∴　 a=-4

8．解：分两种情况讨论：

　 ①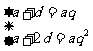 a+aq²-2aq=0，　 ∵　 a≠0，

　　　 ∴ q²-2q+1=0，即q=1，但q=1时，N中的三个元素均相等，此时无解．　 　　　　　　　　　　　

②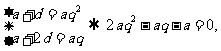

　　　　 ∵　 a≠0， ∴　 2q²-q-1=0

　　　　　 又q≠1，∴　 　，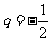

　　　　 ∴　 当M=N 时，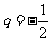

7．解： ①{x|x=2k+1，k∈N}　

　②{(x,y)|x<0，y<0}　　

③{周长为10cm的三角形}

　　　　 ④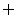

6．{1,2,3,4}

1．D　 2．C　 3．A　 4．B　 5．B

11．解：若x=0，则xy=0，这与集合的互异性矛盾，　　 ∴　 x≠0

若x≠0,xy=0，则y=0，则第二个集合出现两个0元素，这与集合的互异性也矛盾，∴ xy≠0

若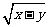=0，则x=y，由两个集合是同一个集合可知xy=|x|，即x²=|x|，得到x=1或-1，但x=1时，y=1，也与集合的互异性也矛盾，所以x=y=-1

∴　 实数x，y的值是确定。

第2课　 集合的表示