3．△ABC中已知∠A=30°cosB=2sinB－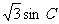

①求证：△ABC是等腰三角形　

②设D是△ABC外接圆直径BE与AC的交点,且AB=2　 求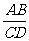：的值

[解]

2．△ABC中已知sin(A+B)+sin(A+B)=,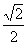

cos(A+B)+cos(A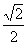+B)= 求角A和B

[解]

[例8]在△ABC中，

求证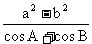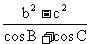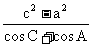： + +=0.

[证明]

追踪训练二

1．△ABC中若面积sinA·cosB－sinB=sinC－sinA·cosC 且周长为12，则其面积最大

值为　　　　 ;

[例7]某观测站C在A城的南偏西20°方向，由A城出发有一条公路定向是南偏东40°，由C处测得距C为31km的公路上B处有1人沿公路向A城以v=5km/h的速度走了4h后到达D处，此时测得C、D间距离为21km。问这人以v的速度至少还要走多少h才能到达A城。

[解]

5.△ABC中A：B：C=1：2：3,

则a：b：c= 　　　　　.　　　　 　　

[选修延伸]

4.△ABC中已知∠A=60°，AB =AC=8：5，面积为10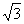，则其周长为　　　　　 ;

3. △ABC中若面积S=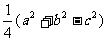

则C=(　 )

A　 　　　B　 　　　C　 　　　D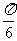

2. △ABC中若sin(A+B)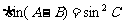 ，则△ABC是(　 )

A 锐角三角形　　 B　 直角三角形　　

C　 钝角三角形　　 D　 等腰三角形

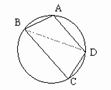
[例6]已知圆内接四边形ABCD的边长分别为AB=2，BC=6，CD=DA=4，求四边形ABCD的面积。

[解]

注：在应用正弦定理解题时要注意方程思想的运

追踪训练一

1. △ABC中a=6,b=6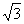 A=30°则边C=(　 )

A、6　　 B、、12　 C、6或12　 D、6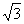

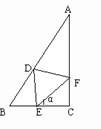
[例2]△ABC中，已知：AB=2，BC=1，CA=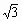，分别在边AB、BC、CA上取点D、E、F，使△DEF是等边三角形.设∠FEC=α，问sinα为何值时，△DEF的边长最短？并求出最短边的长。

分析：要求最短边的长，需建立边长关于角α的目标函数。

[解]

注：在三角形中，已知两角一边求其它边，自然应联想到正弦定理。

[例3]在△ABC中，已知sinB=,

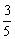　cosA=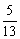, 试求cosC的值。

[解]

[例4]在△ABC中，已知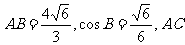边上的中线BD=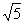，求sinA的值.

分析：本题主要考查正弦定理、余弦定理等基础知识，同时考查利用三角公式进行恒等变形的技能和运算能力.

[解]

[例5]在ΔABC中，角A、B、C所对的边分别为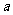、b、c，且.

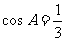　　 (Ⅰ)求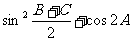的值；

(Ⅱ)若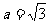，求bc的最大值.

[解]