
1.某汽车运输公司,购买一批豪华大客车投人客运,据市场分析,每辆客车营运的总利润y万元与营运年数n(n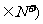 的关系为
的关系为
y=-n2+12n-25,则每辆客车营运( C )年,使其营运年平均利润最大.
A 3 B 4 C 5 D 6
3.已知x>0且x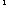 1, y>0且y
1, y>0且y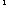 1 , 则logyx+logxy的取值范围是
1 , 则logyx+logxy的取值范围是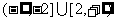
[精典范例]
例1.过点(1 , 2)的直线l与x轴的正半轴、y轴的正半轴分别交于A、B两点, 当△AOB的面积最小时, 求直线l的方程
[解]
见书(但设直线方程可有两种方法).
例2.如图(见书P93) , 一份印刷品的排版面积(矩形)为A , 它的两边都留有宽为a的空白, 顶部和底部都留有宽为b的空白, 如何选择纸张的尺寸, 才能使纸的用量最小?
见书.
思维点拔:
先建立目标函数,然后创造条件利用基本不等式求解。
追踪训练
2.已知a>b>c , n∈N*, 且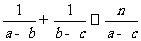 , 则n的最大值为_____4_____
.
, 则n的最大值为_____4_____
.
1.设x>0时, y=3-3x-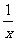 的最大值为
的最大值为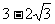
3.进一步开拓视野,认识数学的科学价值和人文价值.
[课堂互动]
自学评价
2.通过对实际问题的研究,进一步体会数学建模的思想。
1.进一步会用基本不等式解决简单的最大(小)值的实际问题。
2. 巨幅壁画画面与地面垂直, 且最高点离地面14米, 最低点离地面2米, 若从离地面1.5米处观赏此画, 问离墙多远时, 视角最大?
巨幅壁画画面与地面垂直, 且最高点离地面14米, 最低点离地面2米, 若从离地面1.5米处观赏此画, 问离墙多远时, 视角最大?
略解:设离墙x米,视角为ψ,
则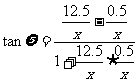 =
=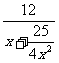
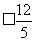
(当x=2.5时等号成立)
答:略.
|
1.建造一个容积为8m3, 深为2m的长方体无盖水池, 如果池底的造价为每平方米120元, 池壁的造价为每平方米80元, 求这个水池的最低造价.
略解:类似于例2,可求得当水池为正方体时,造价最低,为1760元.
2.若半圆的半径为R , 则其半圆上的动点到直径两端点距离之和的最大值为 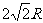 .
.
[精典范例]
例1.用长为4a的铁丝围成一个矩形, 怎样才能使所围矩形的面积最大.(用基本不等式求解).
[解]
见书.
.
例2.某工厂建造一个无盖的长方体贮水池, 其容积为4800m3, 深度为3m , 如果池底每1m2的造价为150元, 池壁每1m2的造价为120元, 怎样设计水池能使总造价最低? 最低总造价为多少元?
见书.
例3.某商场预计全年分批购入每台价值为2000元的电视机共3600台, 每批都购入x台(x为正整数), 且每批需付运费400元, 储存购入的电视机全年所付保管费用与每批购入电视机的总价值(不含运费)成正比, 若每批购入400台, 则全年需用去运费和保管费43600元, 现在全年只有24000元资金可用于支付这笔费用, 能否恰好当地安排每批进货的数量, 使资金够用, 写出你的结论, 并说明理由.
解:设总费用为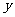 元,保管费用与电视机总价值的比例系数为k(k>0),每批购入x台,则
元,保管费用与电视机总价值的比例系数为k(k>0),每批购入x台,则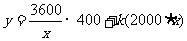 .
.
由于当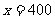 时,
时,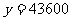 解得
解得
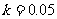 .
.
所以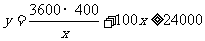 元.
元.
此为所需最低费用.
当且仅当x=120时,取得等号.
因此只需每批购入120台,可使资金够用.
思维点拔:
先建目标函数,再用基本不等式求最值,这是一种很常见题型,加以理解和掌握.
追踪训练
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com