
1.(江苏省启东中学2008年高三综合测试一)集合A={1,2,3,4,5,6},从集合A中任选3个不同的元素组成等差数列,这样的等差数列共有( )
A、4个 B、8个 C、10个 D、12个
答案:D
(二)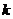 为偶数,则
为偶数,则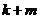 为偶数。则
为偶数。则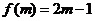 ,
,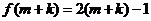 。则
。则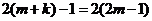 ,解得:
,解得: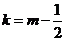 与
与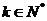 矛盾。 ----(1分)
矛盾。 ----(1分)
由此得:对于给定常数m(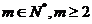 ),这样的
),这样的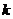 总存在;当
总存在;当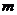 是奇数时,
是奇数时,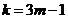 ;当
;当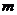 是偶数时,
是偶数时,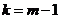 。
----(1分)
。
----(1分)
7.(2009枣庄一模)设数列
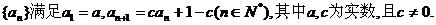
(1)求数列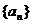 的通项公式;
的通项公式;
(2)设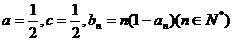 ,求数列
,求数列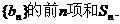
解:(1)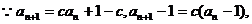
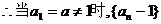 是首项为
是首项为 的等比数列 2分
的等比数列 2分
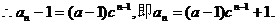 4分
4分
当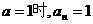 仍满足上式。
仍满足上式。
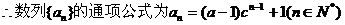
注:未考虑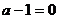 的情况,扣1分。
的情况,扣1分。
(2)由(1)得,当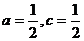 时,
时,
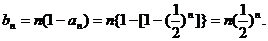 8分
8分
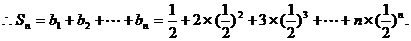
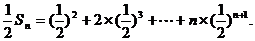
两式作差得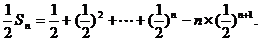
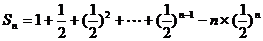
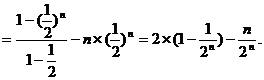
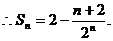 12分
12分
8.(2009冠龙高级中学3月月考)由函数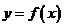 确定数列
确定数列 ,
,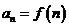 ,函数
,函数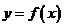 的反函数
的反函数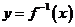 能确定数列
能确定数列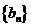 ,
,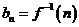 ,若对于任意
,若对于任意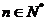 ,都有
,都有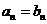 ,则称数列
,则称数列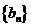 是数列
是数列 的“自反数列”。
的“自反数列”。
(1)若函数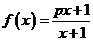 确定数列
确定数列 的自反数列为
的自反数列为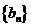 ,求
,求 的通项公式;
的通项公式;
(2)在(1)条件下,记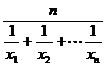 为正数数列
为正数数列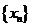 的调和平均数,若
的调和平均数,若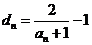 ,
, 为数列
为数列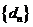 的前
的前 项和,
项和,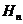 为数列
为数列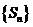 的调和平均数,求
的调和平均数,求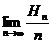 ;
;
(3)已知正数数列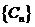 的前
的前 项之和
项之和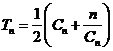 。求
。求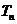 的表达式。
的表达式。
解:(1)由题意的:f –1(x)=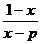 = f(x)=
= f(x)=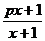 ,所以p = –1,所以an=
,所以p = –1,所以an=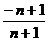
(2) an=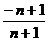 ,dn=
,dn=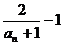 =n,
=n,
Sn为数列{dn}的前n项和,Sn=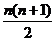 ,又Hn为数列{Sn}的调和平均数,
,又Hn为数列{Sn}的调和平均数,
Hn=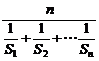 =
=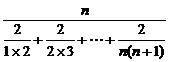 =
=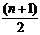
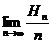 =
=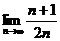 =
=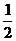
(3)因为正数数列{cn}的前n项之和Tn=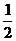 (cn+
(cn+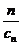 ),
),
所以c1=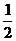 (c1+
(c1+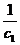 ),解之得:c1=1,T1=1
),解之得:c1=1,T1=1
当n≥2时,cn = Tn–Tn–1,所以2Tn = Tn–Tn–1 +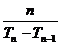 ,
,
Tn +Tn–1 = 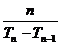 ,即:
,即: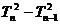 = n,
= n,
所以,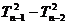 = n–1,
= n–1,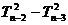 = n–2,……,
= n–2,……,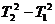 =2,累加得:
=2,累加得:
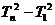 =2+3+4+……+ n,
=2+3+4+……+ n, 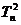 =1+2+3+4+……+ n =
=1+2+3+4+……+ n =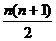 ,Tn=
,Tn=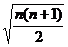
2007--2008年联考题
(一)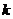 为奇数,则
为奇数,则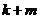 为奇数。则
为奇数。则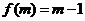 ,
,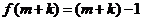 。则
。则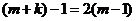 ,解得:
,解得: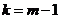 (
(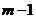 是正奇数)。
----(1分)
是正奇数)。
----(1分)
(二)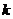 为偶数,则
为偶数,则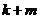 为奇数。则
为奇数。则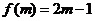 ,
,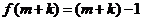 。则
。则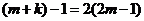 ,解得:
,解得: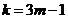 (
(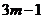 是正偶数)。 ----(1分)
是正偶数)。 ----(1分)
(B)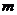 为偶数
为偶数
(一)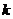 为奇数,则
为奇数,则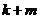 为偶数。则
为偶数。则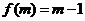 ,
,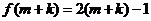 。则
。则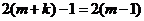 ,解得:
,解得: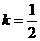 与
与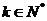 矛盾。
----(1分)
矛盾。
----(1分)
1.(2009上海卢湾区4月模考)已知数列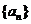 的前
的前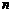 项和为
项和为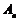 ,且对任意正整数
,且对任意正整数 ,都满足:
,都满足: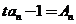 ,其中
,其中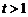 为实数.
为实数.
(1)求数列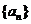 的通项公式;
的通项公式;
(2)若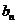 为杨辉三角第
为杨辉三角第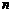 行中所有数的和,即
行中所有数的和,即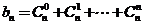 ,
,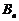 为杨辉三角前
为杨辉三角前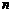 行中所有数的和,亦即为数列
行中所有数的和,亦即为数列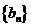 的前
的前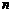 项和,求
项和,求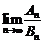 的值.
的值.
解:(1) 由已知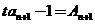 ,
,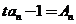 ,相减得
,相减得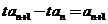 ,由
,由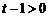 得
得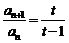 ,又
,又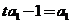 ,得
,得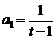 ,故数列
,故数列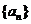 是一个以
是一个以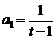 为首项,以
为首项,以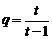 为公比的等比数列.
(4分)
为公比的等比数列.
(4分)
从而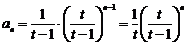
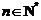 ;
(6分)
;
(6分)
(2)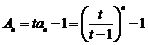 ,
(7分)
,
(7分)
又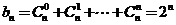 ,故
,故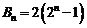 ,
(11分)
,
(11分)
于是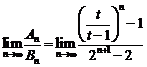 ,
,
当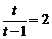 ,即
,即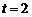 时,
时,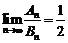 ,
,
当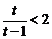 ,即
,即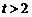 时,
时,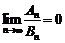 ,
,
当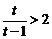 ,即
,即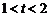 时,
时,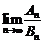 不存在.
(14分)
不存在.
(14分)
2.(2009临沂一模)已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项。
(I) 求数列{an}的通项公式;
(II)
若bn=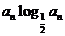 ,sn=b1+b2+┉+bn,求sn+n•
,sn=b1+b2+┉+bn,求sn+n•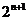 >50成立的正整数 n的最小值。
>50成立的正整数 n的最小值。
解:(I)设等比数列{an}的首项为a1,公比为q,
依题意,有2(a3+2)=a2+a4,
代入a2+a3+a4=28, 得a3=8,
∴a2+a4=20┉┉┉┉┉┉┉┉2分
∴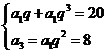 解之得
解之得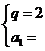 或
或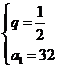 ┉┉┉┉┉┉┉┉4分
┉┉┉┉┉┉┉┉4分
又{an}单调递增,∴q=2,a1=2,
∴an=2n ┉┉┉┉┉┉┉┉6分
(II)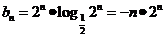 , ┉┉┉┉┉┉┉┉7分
, ┉┉┉┉┉┉┉┉7分
∴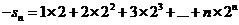 ①
①
∴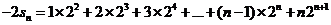 ②
②
∴①-②得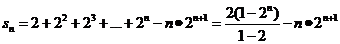 =
=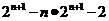 ┉10分
┉10分
∴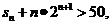 即
即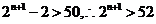
又当n≤4时,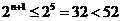 , ┉┉┉┉┉┉┉┉11分
, ┉┉┉┉┉┉┉┉11分
当n≥5时,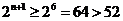 .
.
故使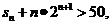 成立的正整数n的最小值为5
. ┉┉┉┉┉┉┉┉12分
成立的正整数n的最小值为5
. ┉┉┉┉┉┉┉┉12分
3.(2009青岛一模)已知等比数列 的前
的前 项和为
项和为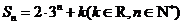
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列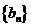 满足
满足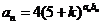 ,
,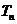 为数列
为数列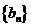 的前
的前 项和,试比较
项和,试比较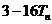 与
与 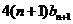 的大小,并证明你的结论.
的大小,并证明你的结论.
解:(Ⅰ)由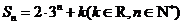 得:
得: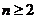 时,
时,
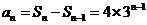 ………………………2分
………………………2分
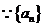 是等比数列,
是等比数列,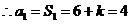
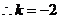 ,得
,得 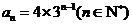 ……4分
……4分
(Ⅱ)由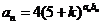 和
和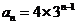 得
得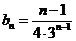 ……………………6分
……………………6分
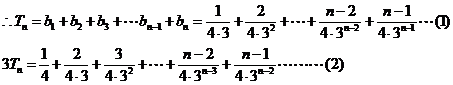
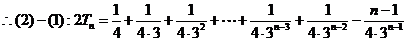
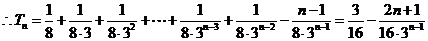 ……10分
……10分
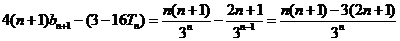
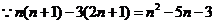 ………………………11分
………………………11分
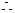 当
当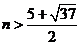 或
或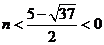 时有
时有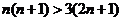 ,所以当
,所以当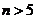
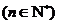 时有
时有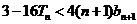
那么同理可得:当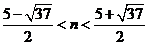 时有
时有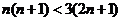 ,所以当
,所以当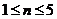
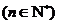 时有
时有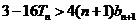 ………………………13分
………………………13分
综上:当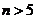
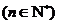 时有
时有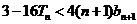 ;当
;当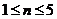
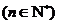 时有
时有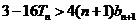 ………………………14分
………………………14分
4.(2009日照一模)已知数列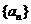 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,对于任意的
项和,对于任意的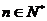 ,满足关系式
,满足关系式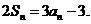
(I)求数列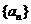 的通项公式;
的通项公式;
(Ⅱ)设数列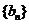 的通项公式是
的通项公式是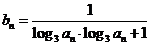 ,前
,前 项和为
项和为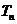 ,求证:对于任意的正整数
,求证:对于任意的正整数 ,总有
,总有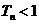
解:(I)由已知得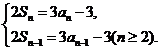
故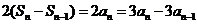
即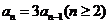
故数列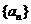 为等比数列,且
为等比数列,且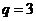
又当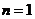 时,
时,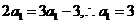
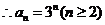 ………………………………6分
………………………………6分
而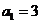 亦适合上式
亦适合上式
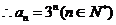 …………………………………8分
…………………………………8分
(Ⅱ)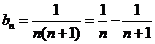
所以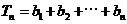
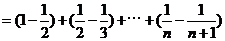
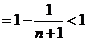 ………………………………12分
………………………………12分
5.(2009泰安一模)已知数列{a }中,
}中,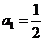 ,点
,点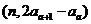 在直线y=x上,其中n=1,2,3….
在直线y=x上,其中n=1,2,3….
(I)
令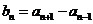 ,求证数列{b
,求证数列{b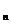 }是等比数列;
}是等比数列;
(II)
球数列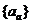 的通项
的通项
解:(I)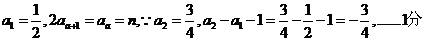
又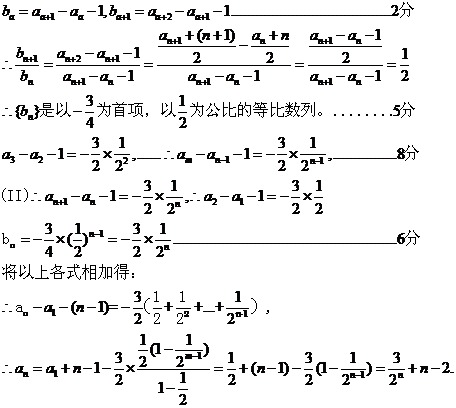
6.(2009上海奉贤区模拟考)已知点集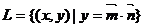 ,其中
,其中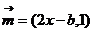 ,
,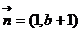 ,点列
,点列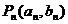 在L中,
在L中,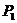 为L与y轴的交点,等差数列
为L与y轴的交点,等差数列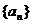 的公差为1,
的公差为1,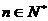 。
。
(1)求数列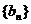 的通项公式;
的通项公式;
(2)若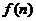 =
= ,令
,令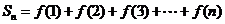 ;试用解析式写出
;试用解析式写出 关于
关于 的函数。
的函数。
(3)若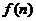 =
= ,给定常数m(
,给定常数m(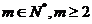 ),是否存在
),是否存在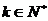 ,使得
,使得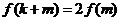 ,若存在,求出
,若存在,求出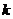 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(1)y=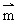 ·
·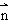 =(2x-b)+(b+1)=2x+1
-----(1分)
=(2x-b)+(b+1)=2x+1
-----(1分)
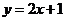 与
与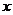 轴的交点
轴的交点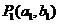 为
为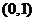 ,所以
,所以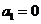 ;
-----(1分)
;
-----(1分)
所以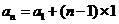 ,即
,即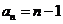 ,
-----(1分)
,
-----(1分)
因为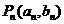 在
在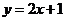 上,所以
上,所以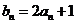 ,即
,即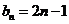 -----(1分)
-----(1分)
(2)设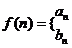
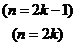 (
(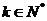 ),
),
即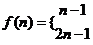
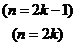 (
(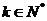 ) ----(1分)
) ----(1分)
(A)当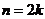 时,
时,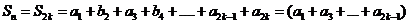
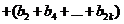 ----(1分)
----(1分)
=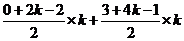 =
=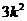 ,而
,而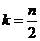 ,所以
,所以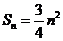 ----(1分)
----(1分)
(B)当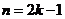 时,
时,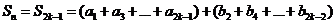 ----(1分)
----(1分)
= 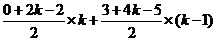 =
=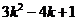 ,
----(1分)
,
----(1分)
而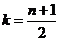 ,所以
,所以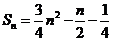 ----(1分)
----(1分)
因此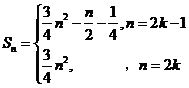 (
(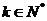 )
----(1分)
)
----(1分)
(3)假设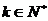 ,使得
,使得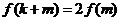 ,
,
(A)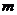 为奇数
为奇数
3. (2009上海九校联考)已知数列 的前
的前 项和为
项和为 ,若
,若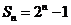 ,则
,则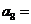 .
.
答案 128
2.(2009闵行三中模拟)已知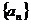 是等比数列,
是等比数列,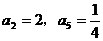 ,则
,则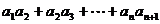 = 。
= 。
答案 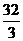 (
(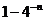 )
)
1.(2009冠龙高级中学3月月考)若数列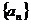 中,
中,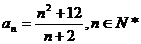 ,则数列
,则数列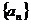 中的项的最小值为_________。
中的项的最小值为_________。
答案 4
3.(2009日照一模)设 是等差数列
是等差数列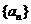 的前
的前 项和,若
项和,若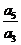 =
=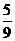 ,则
,则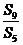 等于
等于
A 1 B.-1 C.2 D.
1 B.-1 C.2 D.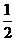
答案A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com