
20.(2009重庆卷理)设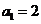 ,
,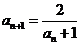 ,
,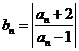 ,
,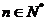 ,则数列
,则数列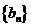 的通项公式
的通项公式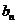 =
.
=
. 



解析 由条件得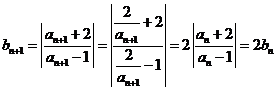 且
且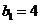 所以数列
所以数列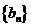 是首项为4,公比为2的等比数列,则
是首项为4,公比为2的等比数列,则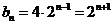
答案 2n+1
19.(2009湖南卷理)将正⊿ABC分割成
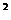 (
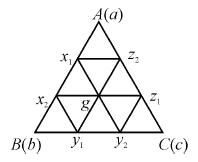
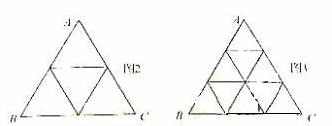
( ≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别一次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,f(3)=
≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别一次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,f(3)= 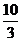 ,…,f(n)=
,…,f(n)= 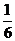 (n+1)(n+2)
(n+1)(n+2) 

答案 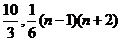
解析 当n=3时,如图所示分别设各顶点的数用小写字母表示,即由条件知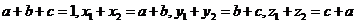
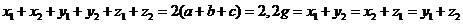
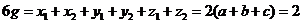


即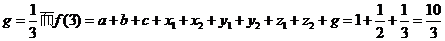
进一步可求得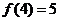 。由上知
。由上知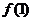 中有三个数,
中有三个数,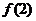 中
有6个数,
中
有6个数,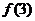 中共有10个数相加 ,
中共有10个数相加 ,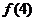 中有15个数相加….,若
中有15个数相加….,若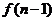 中有
中有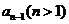 个数相加,可得
个数相加,可得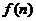 中有
中有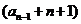 个数相加,且由
个数相加,且由
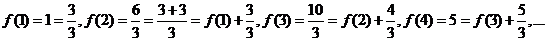
可得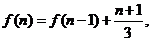 所以
所以
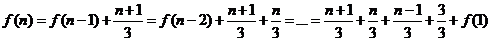
=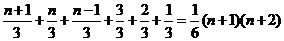
18.(2009宁夏海南卷文)等比数列{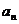 }的公比
}的公比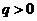 , 已知
, 已知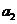 =1,
=1,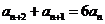 ,则{
,则{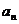 }的前4项和
}的前4项和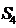 =
= 

解析 由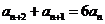 得:
得: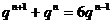 ,即
,即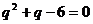 ,
,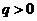 ,解得:q=2,又
,解得:q=2,又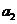 =1,所以,
=1,所以,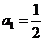 ,
,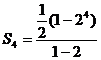 =
=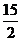 。
。
答案 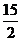
17.(2009陕西卷理)设等差数列 的前n项和为
的前n项和为 ,若
,若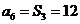 ,则
,则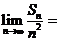 .
.
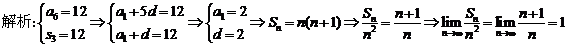
答案:1
16.(2009陕西卷文)设等差数列 的前n项和为
的前n项和为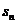 ,若
,若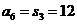 ,则
,则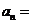 .
. 

解析:由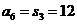 可得
可得 的公差d=2,首项
的公差d=2,首项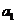 =2,故易得
=2,故易得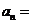 2n.
2n.
答案:2n
15.(2009宁夏海南卷理)等差数列{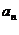 }前n项和为
}前n项和为 。已知
。已知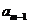 +
+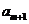 -
-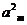 =0,
=0,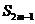 =38,则m=_______
=38,则m=_______
解析由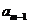 +
+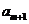 -
-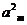 =0得到
=0得到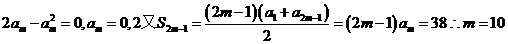 。
。
答案10
14.(2009湖北卷理)已知数列 满足:
满足: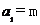 (m为正整数),
(m为正整数),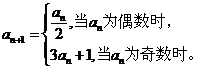 若
若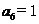 ,则m所有可能的取值为__________。
,则m所有可能的取值为__________。 

答案 4 5 32
解析 (1)若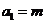 为偶数,则
为偶数,则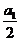 为偶, 故
为偶, 故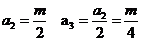
①当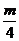 仍为偶数时,
仍为偶数时,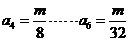 故
故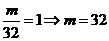
②当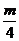 为奇数时,
为奇数时,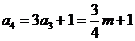
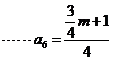
故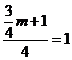 得m=4。
得m=4。
(2)若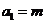 为奇数,则
为奇数,则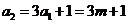 为偶数,故
为偶数,故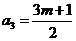 必为偶数
必为偶数
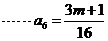 ,所以
,所以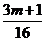 =1可得m=5
=1可得m=5
13.(2009山东卷文)在等差数列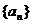 中,
中,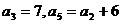 ,则
,则 .
.
解析 设等差数列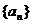 的公差为
的公差为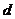 ,则由已知得
,则由已知得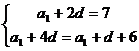 解得
解得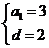 ,所以
,所以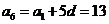 .
. 

答案:13.
[命题立意]:本题考查等差数列的通项公式以及基本计算.
12..(2009江苏卷)设 是公比为
是公比为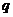 的等比数列,
的等比数列,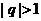 ,令
,令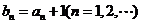 ,若数列
,若数列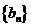 有连续四项在集合
有连续四项在集合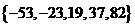 中,则
中,则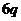 =
.
=
.
答案 -9
解析 考查等价转化能力和分析问题的能力。等比数列的通项。

 有连续四项在集合
有连续四项在集合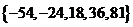 ,四项
,四项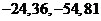 成等比数列,公比为
成等比数列,公比为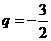 ,
,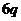 = -9
= -9
11.(2009北京理)已知数列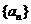 满足:
满足: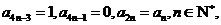 则
则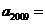 ________;
________;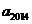 =_________.
=_________.
答案 1,0
解析 本题主要考查周期数列等基础知识.属于创新题型.
依题意,得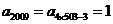 ,
,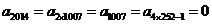 .
. 

∴应填1,0.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com