
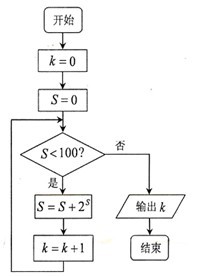
 2009年高考题
2009年高考题
20.(2007山西实验中学模拟)正项数列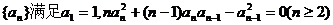
(1)求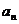 ;
;
(2)试确定一个正整数N,使当n>N时,不等式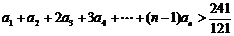
成立;
(3)求证: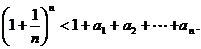
解:(1)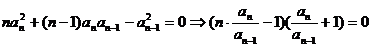
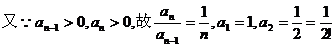
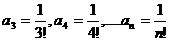 ………………………………4分
………………………………4分
(2)由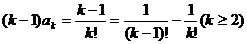
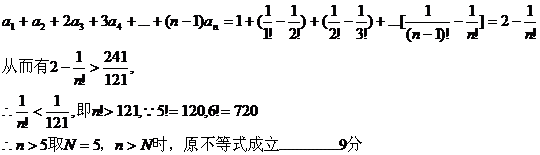 (3)将
(3)将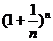 展开,
展开,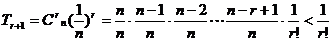
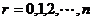
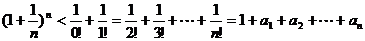 …………14
…………14
19.(2007江苏省南京市) 14.已知正项数列{ an }满足Sn+Sn-1=ta+2 (n≥2,t>0),a1=1,其中Sn是数列{ an }的前n项和.
(Ⅰ)求通项an;
(Ⅱ)记数列{}的前n项和为Tn,若Tn<2对所有的n∈N*都成立.求证:0<t≤1
解:∵a1=1 由S2+S1=ta+2,得a2 =ta,∴a2 =0(舍)或a2=,
Sn+Sn-1=ta+2 ① Sn-1+Sn-2=ta+2 (n≥3) ②
①-②得an+an-1=t(a -a)(n≥3),(an+an-1)[1-t(an-an-1)] =0,
由数列{ an }为正项数列,∴an+an-1≠0,故an-an-1=(n≥3),
即数列{ an }从第二项开始是公差为的等差数列.
∴an=
(2)∵T1=1<2,当n≥2时,Tn=t++++ …+=t+ t2(1-) =t+ t2
要使Tn<2,对所有的n∈N*恒成立,只要Tn=t+ t2 < t+ t2≤2成立,∴0<t≤1.
18.(湖北省黄冈市麻城博达学校2008届三月综合测试)把正奇数数列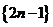 中的数按上小下大、左小右大的原则排成如下三角形数表:
中的数按上小下大、左小右大的原则排成如下三角形数表:
1
3 5
7 9 11
- - - -
- - - - -
设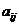 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第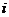 行,从左往右数第
行,从左往右数第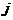 个数。
个数。
(Ⅰ)若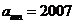 ,求
,求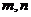 的值;
的值;
(Ⅱ)已知函数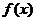 的反函数
的反函数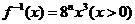 为,若记三角形数表中从上往下数第
为,若记三角形数表中从上往下数第 行各数的和为
行各数的和为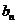 ,求数列
,求数列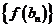 的前
的前 项和
项和 。
。
解:(Ⅰ)∵三角形数表中前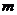 行共有
行共有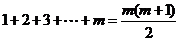 个数,
个数,
∴第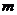 行最后一个数应当是所给奇数列中第
行最后一个数应当是所给奇数列中第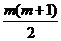 项,即
项,即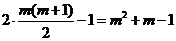 。
。
因此,使得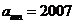 的
的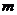 是不等式
是不等式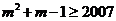 的最小正整数解。
的最小正整数解。
由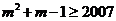 得
得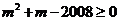 ,∴
,∴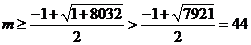 。∴
。∴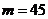 。
。
第45行第一个数是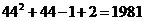 ,∴
,∴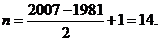
(Ⅱ)∵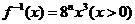 ,∴
,∴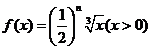 。
。
∵第 行最后一个数是
行最后一个数是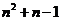 ,且有
,且有 个数,若
个数,若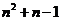 将看成第
将看成第 行第一个数,则第
行第一个数,则第 行各数成公差为
行各数成公差为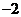 的等差数列,故
的等差数列,故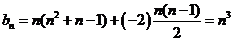 。∴
。∴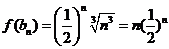 。
。
故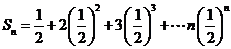 。用错位相减法可求得
。用错位相减法可求得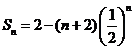
17.(北省三校联合体高2008届2月测试)已知数列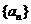 的首项
的首项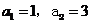 ,前
,前 项和为
项和为 ,且
,且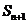 、
、 、
、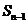 分别是直线
分别是直线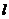 上的点A、B、C的横坐标,点B分
上的点A、B、C的横坐标,点B分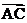 所成的比为
所成的比为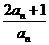 ,设
,设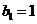
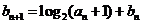 。
。
⑴ 判断数列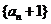 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
⑵ 设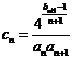 ,证明:
,证明: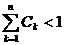 。
。
解 ⑴由题意得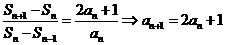 ……………3分
……………3分
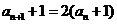
 数列
数列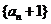 是以
是以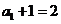 为首项,以2为公比的等比数列。………………6分
为首项,以2为公比的等比数列。………………6分
则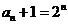
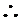
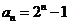 (
(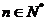 )]
)]
⑵由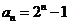 及
及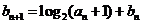 得
得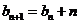
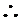
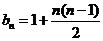 ,……………………………………………………………8分
,……………………………………………………………8分
则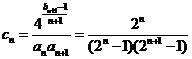
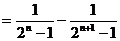 ……………………10分
……………………10分
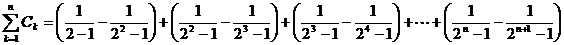
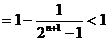 ………………12分
………………12分
16.(黑龙江省哈尔滨九中2008年第三次模拟考试)已知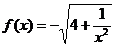 数列
数列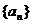 的前n项和为
的前n项和为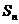 ,点
,点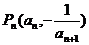 在曲线
在曲线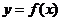 上
上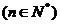 且
且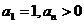 .
.
(1)求数列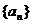 的通项公式;
的通项公式;
(2)数列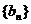 的前n项和为且
的前n项和为且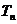 满足
满足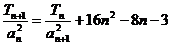 ,设定
,设定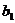 的值使得数
的值使得数
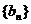 是等差数列;
是等差数列;
(3)求证: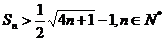 .
.
解:(1)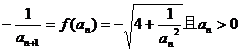
∴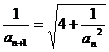
∴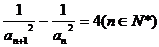
∴数列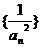 是等差数列,首项
是等差数列,首项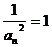 公差d=4
公差d=4
∴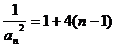
∴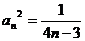
∵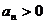
∴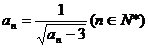 …………(4分)
…………(4分)
(2)由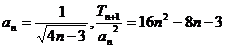
得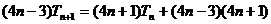
∴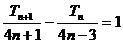
∴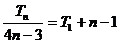
∴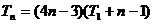
若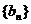 为等差数列,则
为等差数列,则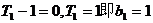
∴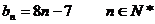
(3)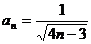
∴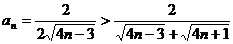
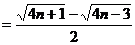
∴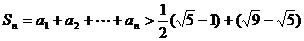
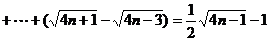
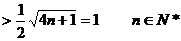 ……………………12分
……………………12分
15.(黑龙江省哈师大附中2008届高三上期末)将正整数按下表的规律排列,把行与列交叉处的一个数称为某行某列的数,记作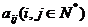 ,如第2行第4列的数是15,记作a24=15,则有序数对(a28,a84)是
。
,如第2行第4列的数是15,记作a24=15,则有序数对(a28,a84)是
。
1 4 5 16 17 36 ……
2 3 6 15 18 35 ……
9 8 7 14 19 34 ……
10 11 12 13 20 33 ……
25 24 23 22 21 32 ……
26 27 28 29 30 31 ……
…… …… …… …… ……
答案:(63,53)
14.(河南省上蔡一中2008届高三月考)如图,在直角坐标系中,一质点从原点出发,沿图示箭头方向每秒钟移动一个单位,问第2008秒时质点所在的位置坐标是
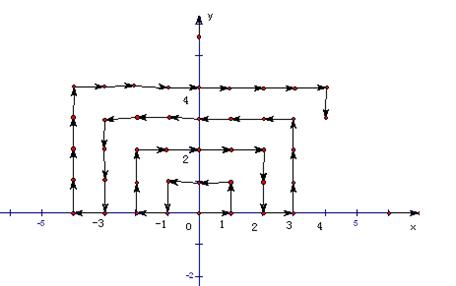
答案:(-31,7)
13.(北京市十一学校2008届高三数学练习题)一次展览会上展出一套由宝石串联制成的工艺品,如图所示.若按照这种规律依次增加一定数量的宝石, 则第5件工艺品所用的宝石数为 颗;第 件工艺品所用的宝石数为 颗 (结果用
件工艺品所用的宝石数为 颗 (结果用 表示).
表示).

|
|
||||||
|
|||||||
|
|||||||
答案:66,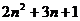
12.(2008江苏省启东中学高三综合测试三)如图,第n个图形是由正n+2边形“扩展”而来,(n=1,2,3,…),则第n-2个图形中共有 个顶点。
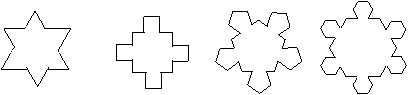
答案:n2+n
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com