1．一个面积为的等腰梯形，上底长为，下底长为上底长的倍，则它的高与的函数关系是　　　　　　　 (　 )

7．求函数的值域．

本节学习疑点：

6．作出函数的图象，其中，表示不超过的最大整数，如，．

5．求下列函数的定义域，值域，并画出图象：

(1)；(2)．

拓展延伸

4．函数的图象如图所示，填空：

(1)　　　　 ；

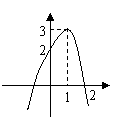(2)　　　　 ；

(3)　　　　 ；

(4)若，

则与的大小关系为　　　 　　　．

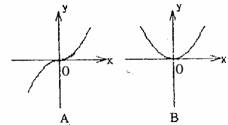
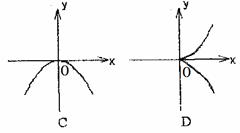
3．函数的图象大致是　　　 (　 )　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

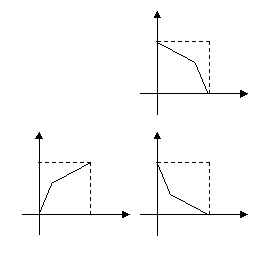
2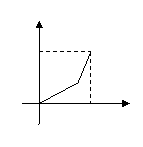．郑强去上学，先跑步，后步行，如果表示郑强离学校的距离，表示出发后的时间，则下列图象中符合郑强走法的是　 (　 )

1．若二次函数的图象的对称轴是直线，则　　　　　　　　 (　 )

11．已知某商品的价格上涨，销售的数量就减少，其中为正的常数．

(1)当时，该商品的价格上涨多少，就能使销售的总金额最大？

(2)如果适当地涨价，能使销售总金额增加，求的取值范围．

10．经市场调查，某商品在近天内，其销售量和价格均为时间的函数，且销售量近似地满足关系，在前天里价格为

，

在后天里价格为

，

求这种商品的日销售额的最大值.

拓展延伸