
2.(1)
(2)

(3)当 时,
时,
 ,
,
当 时,
时, 

(4)


4.解不等式:
(1)
(2)
答案:1.略
3.解下列方程:
(1) (2)
(2)
(3)
(4)
2. 比较下列各组数中两个值的大小:
(1) ,
, ;
;
(2) ,
, ;
;
(3) ,
, .
.
(4) ,
, ,
,
1.求函数 的定义域,并画出函数的图象。
的定义域,并画出函数的图象。
5.一般地,如果函数 存在反函数,那么它的反函数,记作
存在反函数,那么它的反函数,记作
思考:互为反函数的两个函数的定义域和值域有什么关系?
原函数的定义域和值域分别是反函数的值域和定义域。
[精典范例]
例1:求下列函数的定义域
(1) ;
;
(2)
 ;
;
(3)
(4)
[分析]:此题主要利用对数函数 的定义域
的定义域 求解。
求解。
(1)由 得
得 ,
,
∴函数的 定义域是
定义域是 ;
;
(2)由 得
得 ,
,
∴函数

的定义域是
(3) 得
得
 或
或
∴函数 的定义域是
的定义域是
(4)由 得
得
∴ ,函数
,函数 的定义域是
的定义域是
例2:利用对数函数的性质,比较下列各组数中两个数的大小:
(1) ,
, ; (2)
; (2) ,
, ;
;
(3) ,
, ; (4)
; (4) ,
, ,
,
[解](1)对数函数 在
在 上是增函数,
上是增函数,
于是
 ;
;
(2)对数函数 在
在 上是减函数,
上是减函数,
于是
 ;
;
(3).∵ ,
,
 ,
,

 ;
;
(4)∵ ,
,
而
∴

 (1)
(1)
点评: 本例是利用对数函数的增减性比较两个对数的大小,当不能直接进行比较时,可在两个对数中间插入一个已知数(如1 或0),间接比较上述两个对数的大小。
例3若
 且
且 ,求
,求 的取值范围
的取值范围
(2)已知 ,求
,求 的取值范围;
的取值范围;
[解](1)当 时
时 在
在 上是单调增函数,
上是单调增函数,


当 时
时 在
在 上是单调减函数,
上是单调减函数,


综上所述: 的取值范围为
的取值范围为
(2)当 ,即
,即 时
时
由 , 解得:
, 解得:

∴
当 ,即
,即 时
时
由 , 解得:
, 解得:
 ,此时无解。
,此时无解。
综上所述: 的取值范围为
的取值范围为
点评:本题的关键是利用对数函数的单调性解不等式,一定要注意对数函数定义域。
追踪训练一
4.指数函数
 与对数函数
与对数函数
 称为互为反函数。
称为互为反函数。
指数函数的定义域和值域分别是对数函数的值域和定义域。
3. 对数函数的图象与指数函数的图象
关于直线 对称。
对称。
画对数函数
 的图象,可以通过作
的图象,可以通过作
 关于直线
关于直线 的轴对称图象获得,但在一般情况下,要画给定的对数函数的图象,这种方法是不方便的。所以仍然要掌握用描点法画图的方法,注意抓住特殊点(1,0)及图象的相对位置。
的轴对称图象获得,但在一般情况下,要画给定的对数函数的图象,这种方法是不方便的。所以仍然要掌握用描点法画图的方法,注意抓住特殊点(1,0)及图象的相对位置。
2. 对数函数的性质为
|
图 象 |
 |
 |
|
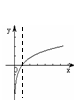 |

|
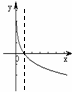


 ,即当
,即当 时,
时,
 上是减函数
上是减函数1. 对数函数的定义:
函数 
 叫做对数函数(logarithmic function),
叫做对数函数(logarithmic function),
定义域是 
思考:函数 与函数
与函数
 的定义域、值域之间有什么关系?
的定义域、值域之间有什么关系?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com