1．如图，海岸线，现用长为的拦网围成一养殖场，其中．

(1)若,求养殖场面积最大值；

(2)若、为定点，，在折线内选点，　　 使，求四边形养殖场DBAC的最大面积．

4．设数列是一个严格递增的正整数数列．

(1) 若是该数列的其中两项，求证: ;

(2) 若该数列的两个子数列和都是等差数列，求证:这两个子数列的公差相等;

(3) 若(2)中的公差为1，求证: ,并证明数列也是等差数列．

3．已知等差数列的首项为，公差为，等比数列的首项为，公比为(其中均为正整数)．

(1)若求数列、的通项公式；

(2)在(1)的条件下，若成等比数列，求数列的通项公式；

(3)若且至少存在三个不同的值使得等式N)成立，试求、的值．

2．已知数列的前n项和为，数列是公比为2的等比数列．

(1)证明：数列成等比数列的充要条件是；

(2)设N^*)．若对 N^*恒成立，求的取值范围．

1．已知等差数列{A_N}的首项为a，公差为b，等比数列{B_N}的首项为b，公比为a，其中a,b都是大于1的正整数，且a₁<b₁，b₂<a₃．

(1)求a的值；

(2)若对于任意的 N^*，总存在N^*，使得成立，求b的值；

(3)令，问数列中是否存在连续三项成等比数列？若存在，求出所有成等比数列的连续三项；若不存在，请说明理由．

4．函数．

(1)求函数的极值；

(2)已知在上是增函数，求的取值范围；

(3)在上最大值与最小值之差为，求的最小值．

3．已知函数，(，且)．

(1)当时，求函数的单调区间；

(2)求函数在区间上的最小值．

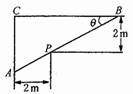
2．某直角走廊的示意图如图所示，其两边走廊的宽度均为2m．

(1)过点的一条直线与走廊的外侧两边交于两点，且与走廊的一边的夹角为，将线段的长度表示为的函数；

(2)一根长度为5m的铁棒能否水平(铁棒与地面平行)通过该直角走廊？请说明理由(铁棒的粗细忽略不计)．

1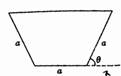． 汶川大地震后，为了消除某堰塞湖可能造成的危险，救授指挥部商定，给该堰塞湖挖一个横截面为等腰梯形的简易引水槽(如图所示)进行引流，已知等腰梯形的下底与腰的长度都为，且水槽的单位时间内的最大流量与横载面的面积为正比，比例系数．

(1)试将水槽的最大流量表示成关于的函数；

(2)为确保人民的生命财产安全，请你设计一个方案，使单位时间内水槽的流量最大(即当为多大时，单位时间内水槽的流量最大)．

4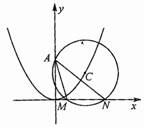．已知圆C的圆心在抛物线上运动，且圆C过点，若MN为圆C在轴上截得的弦.

(1)求弦长；

(2)设，求的取值范围．