21．(本小题满分13分)

已知抛物线的焦点为F，以点为圆心，|AF|为半径的圆在x轴的上方与抛物线交于M、N两点。

　 (I)求证：点A在以M、N为焦点，且过点F的椭圆上；

　 (II)设点P为MN的中点，是否存在这样的a，使得|FP|是|FM|与|FN|的等差中项？如果存在，求出实数a的值；如果不存在，请说明理由。

20．(本小题满分13分)

已知函数的图象有公共点，且在该点处的切线相同。

　 (I)用a表示b，并求b的最大值；

　 (II)求证：

19．(本小题满分13分)

已知函数

　 (I)求数列的通项公式；

　 (II)若数列

18．(本小题满分12分)

　　 某地区举行环保知识大赛，比赛分初赛和决赛两部分，初赛采用选用选一题答一题的方式进行，每位选手最多有5次选题答题的机会，选手累计答对3题或答错3题即终止其初赛的比赛，答对3题直接进入决赛，答错3次者则被淘汰，已知选手甲连续两次

答错的概率为(已知甲回答每个问题的正确率相同，且相互之间没有影响)

　 (I)求甲选手回答一个问题的正确率；

　 (II)求选手甲进入决赛的概率；

　 (III)设选手甲在初赛中的答题的个数为并求出的数学期望。

17．(本小题满分12分)

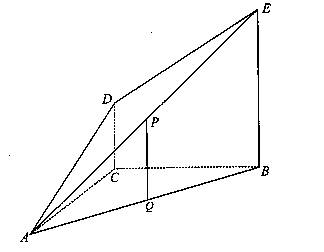
如图，DC⊥平面ABC，EB//DC，AC=BC=EB=2DC=2，∠ACB=120°，P，Q分别为AE、AB的中点。

　 (I)证明：PQ//平面ACD；

　 (II)求异面直线AE与BC所成角的余弦值；

　 (III)求平面ACD与平面ABE所成锐二面角的大小。

16．(本小题满分12分)

　　 若向量，在函数

的图象中，对称中心到对称轴的最小距离为且当的最大值为1。

　 (I)求函数的解析式；

　 (II)求函数的单调递增区间。

15．由曲线所围成的图形的面积的最小值是　　 。

14．等差数列的最大值是　　　　　 。

13．若的展开式中含有常数项，则n的最小值等于　　　 。

12．在极坐标系中，过点的切线，则切线的极坐标方程是　　　 。