3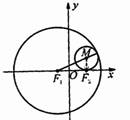．已知圆，定点动圆过点，且与圆相内切．

(1)求点M的轨迹C的方程；

(2)若过原点的直线与(1)中的曲线C交于A，B两点，且的面积为，

求直线的方程．

2．已知A、B是椭圆的左、右顶点，直线交椭圆于M、N两点，经过A、M、N的圆的圆心为，经过B、M、N的圆的圆心为．

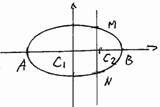(1)求证为定值；

(2)求圆与圆的面积之和的取值范围．

1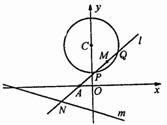．已知过点的动直线与圆相交于两点，是中点，与直线相交于．

(1)求证：当与垂直时，必过圆心;

(2)当时，求直线的方程;

(3)探索是否与直线的倾斜角有关?若无关，请求出其值；若有关，请说明理由．

3．从一副扑克牌的红桃花色中取5张牌，点数分别为1，2，3，4，5． 甲、乙两人玩一种游戏：甲先取一张牌，记下点数，放回后乙再取一张牌，记下点数． 如果两个点数的和为偶数就算甲胜，否则算乙胜．

(1)求甲胜且点数的和为6的事件发生的概率；

(2)这种游戏规则公平吗？说明理由．

2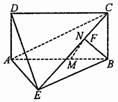．如图，四边形ABCD为矩形，BC⊥平面ABE，F为CE上的点，且BF⊥平面ACE．

(1)求证：AE⊥BE；

(2)设点M为线段AB的中点，点N为线段CE的中点，求证：　　　 MN //平面DAE．

1．已知在△ABC中，a、b、c分别为角A、B、C所对的边，向量，，．

(1)求角A的大小；

(2)若a=3，求△ABC面积的最大值．

8．已知F₁、F₂分别是椭圆，的左、右焦点，以原点O为圆心，OF₁为半径的圆与椭圆在y轴左侧交于A、B两点，若△F₂AB是等边三角形，则椭圆的离心率等于　　　　 ．

7. 当x∈(1，3)时，不等式x²+mx+4<0恒成立，则m的取值范围是　 　　　.

6. 已知，函数的最小值是 　　　　.

5．若，，则对任意，使的概率为　　 ．