23．必做题, 本小题10分．解答时应写出文字说明、证明过程或演算步骤．

已知函数，．

(1)证明：当时，；

(2)求函数的的极值．

22. 必做题, 本小题10分．解答时应写出文字说明、证明过程或演算步骤．

如图，在三棱柱中，，顶点在底面上的射影恰为点B，且．

(1)求棱与BC所成的角的大小；

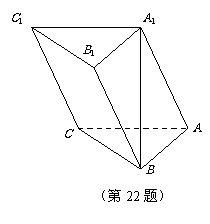(2)在棱上确定一点P，使，并求出二面角的平面角的余弦值．

21．(选做题)在A，B，C，D四小题中只能选做2题，每小题10分，共计20分．请在答题卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．

A．选修4－1　几何证明选讲

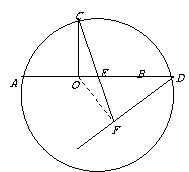
如图，是⊙的直径，是⊙上的两点，

⊥，过点作⊙的切线FD交的延长

线于点．连结交

于点.

　 　求证：.

B．选修4－2　矩阵与变换

求矩阵的特征值及对应的特征向量.

C．选修4－4　坐标系与参数方程

已知曲线的极坐标方程是，直线的参数方程是(为参数)．

　 (1)将曲线的极坐标方程化为直角坐标方程；

　 (2)设直线与轴的交点是，是曲线上一动点，求的最大值.

D．选修4－5　不等式选讲

　　　　 设均为正数，且，求证

20．(本题满分16分)

已知函数，，且)．

(1)讨论函数的单调性；

(2)若，关于的方程有唯一解，求a的值.

_{数学试卷　 第4页(共4页)}

19. (本题满分16分)

设数列{a_n}是由正数组成的等比数列，公比为q，S_n是其前n项和．

(1)证明；

　　 (2)设记数列的前n项和为T_n，试比较q²S_n和T_n的大小.

18. (本题满分15分)

在平面直角坐标系xOy中，已知对于任意实数，直线恒过定点F. 设椭圆C的中心在原点，一个焦点为F，且椭圆C上的点到F的最大距离为.

(1)求椭圆C的方程；

(2)设(m，n)是椭圆C上的任意一点，圆O：与椭圆C有4个相异公共点，试分别判断圆O与直线l₁：mx+ny=1和l₂：mx+ny=4的位置关系.

17. (本题满分15分)

田忌和齐王赛马是历史上有名的故事. 设齐王的3匹马分别为A、B、C，田忌的3匹马分别为a，b，c，6匹马的奔跑速度由快到慢的顺序依次为：A，a，B，b，C，c. 两人约定：6匹马均需参赛，共赛3场，每场比赛双方各出1匹马，最终至少胜两场者为获胜.

　 (1)如果双方均不知道对方的出马顺序，求田忌获胜的概率；

　 (2)颇有心计的田忌赛前派探子到齐王处打探实情，得知齐王第一场必出A马. 那么，田忌应怎样安排马的出场顺序，才能使获胜的概率最大？

_{数学试卷 　第3页 (共4页)}

16. (本题满分14分)

如图，已知四边形ABCD为矩形，平面ABE，AE=EB=BC=2,

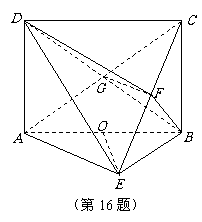F为CE上的点，且平面ACE.

(1)求证：AE//平面BDF；

(2)求三棱锥D－ACE的体积.

15. (本题满分14分)

已知向量与共线，其中A是△ABC的内角．

(1)求角的大小；

(2)若BC=2，求△ABC面积的最大值，并判断S取得最大值时△ABC的形状.

_{数学试卷　 第2页(共4页)}

14.数列满足：，若数列有一个形如的通项公

式，其中均为实数，且，则 ▲ .(只要写出一个通项公

式即可)