20．(本小题满分16分)

(Ⅰ)∵在上存在最大值和最小值，

　　　　　　　 ∴(否则值域为R)，

　　　 ∴

　　　　　　　 ，

又，由题意有，

　　　　　　　 ∴；　　 (4分)

　　　 (Ⅱ)若为奇函数，∵，∴，

题7．(2010年江苏省苏北四市高三年级第二次模拟考试)已知函数(不同时为零的常数)，导函数为.

(1)当时，若存在使得成立，求的取值范围；

(2)求证：函数在内至少有一个零点；

(3)若函数为奇函数，且在处的切线垂直于直线，关于的方程在上有且只有一个实数根，求实数的取值范围

当时，，故．

所以所求的取值范围是或．

题8．(泰州市2010届高三联考试题)(本小题满分16分)

已知函数，(其中为常数)；

(1)如果函数和有相同的极值点，求的值；

(2)设，问是否存在，使得，若存在，请求出实数的取值范围；若不存在，请说明理由．

(3)记函数，若函数有5个不同的零点，求实数的取值范围．

题9．(洪泽中学2010年4月高三年级第三次月考试卷对于定义在区间D上的函数，若存在闭区间和常数，使得对任意，都有，且对任意∈D，当时，恒成立，则称函数为区间D上的“平底型”函数.

(1)判断函数和是否为R上的“平底型”函数？　　 并说明理由；

(2)设是(1)中的“平底型”函数，为非零常数，若不等式 对一切R恒成立，求实数的取值范围；

(3)若函数是区间上的“平底型”函数，求和的值.

7. (2010年江苏省苏北四市高三年级第二次模拟考试)已知函数(为常数且)，若在区间的最小值为，则实数的值为　　 ▲　 .

题19．(2010年苏北四市高三年级第二次模拟考试)若函数的定义域和值域均为，则的取值范围是 ▲ ___.

题20．(南京市2010年3月高三第二次模拟)定义在R上的满足=则　　　 。

题21．(南京市2010年3月高三第二次模拟)已知定义域为D的函数f(x),如果对任意x∈D,存在正数K, 都有∣f(x)∣≤K∣x∣成立，那么称函数f(x)是D上的“倍约束函数”，已知下列函数：①f(x)=2x②=；③=；④=，其中是“倍约束函数的是　　　 。①③④

题22．(南京市2010年3月高三第二次模拟)定义在R上的奇函数,当x∈(0，+∞)时，f(x)=,则不等式f(x)<-1的解集是　　　　 。

题23．(洪泽中学2010年4月高三年级第三次月考试卷已知映射.设点，，点M 是线段AB上一动点，.当点M在线段AB上从点A开始运动到点B结束时，点M的对应点所经过的路线长度为 　　　　　　

题1．(南通市2010年高三二模)(本小题满分16分)

设函数f(x)＝x⁴+bx²+cx+d，当x＝t₁时，f(x)有极小值．

(1)若b＝－6时，函数f(x)有极大值，求实数c的取值范围；

(2)在(1)的条件下，若存在实数c，使函数f(x)在闭区间［m－2，m+2］上单调递增，求实数m的取值范围；

(3)若函数f(x)只有一个极值点，且存在t₂∈(t₁，t₁+1)，使f ′(t₂)＝0，证明：函数g(x)＝f(x)－x²+t₁x在区间(t₁，t₂)内最多有一个零点．

题2．(江苏省南通市2010年高三二模)(本小题满分16分)

如图所示的自动通风设施．该设施的下部ABCD是等腰梯形，其中AB=1米，高0.5米，CD=2a(a＞)米．上部CmD是个半圆，固定点E为CD的中点．△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风)，MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆．

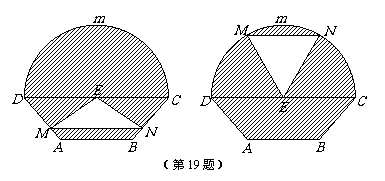(1)设MN与AB之间的距离为x米，试将三角通风窗EMN的通风面积S(平方米)表示成关于x的函数；

(2)当MN与AB之间的距离为多少米时，三角通风窗EMN的通风面积最大？并求出这个最大面积．

当时，．……………………………………………14分

综上，时，当时，，即MN与AB之间的距离为0米时，三角通风窗EMN的通风面积最大，最大面积为平方米．时，当时，， 即与之间的距离为米时，三角通风窗EMN的通风面积最大，最大面积为平方米．………………………16分

题3．(2010年3月苏、锡、常、镇四市高三教学情况调查一)(本小题满分16分)

　　 已知函数(，实数，为常数)．

(1)若()，且函数在上的最小值为0，求的值；

(2)若对于任意的实数，，函数在区间上总是减函数，对每个给定的n，求的最大值h(n)．

设g(x)=，

题3．(无锡市2010年普通高中高三质量调研)(本题满分16分)

　　　 已知函数为奇函数，

且在处取得极大值2

　 (1)求函数的解析式；

　 (2)记，求函数的单调区间；

　 (3)在(2)的条件下，当时，若函数的图像的直线的下方，求的取值范围。

解析：(1)由(≠0)为奇函数，

　　　 ∴，代入得，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 1分

　　　 ∴，且在取得极大值2

　　　 ∴　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 3分

　　　 解得，，∴　　　　　　　　　　　　　　　　　　　　　　　　　　　 4分

　 (2)∵，

　　　 ∴　　　　　　　　　　　　　　　　　　　　　　　　　　 5分

　　　 因为函数定义域为(0，+∞)，所以

　　　 得，(舍去).

　　　 由函数定义域为(0，+∞)，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 13分

　　　 则当时，，当时，

　　　 ∴当时，函数取得最小值1-。　　　　　　　　　　　　　　　　　　　　　　　　　　 15分

　　　 故的取值范围是(1，+∞)。答也正确　 16分

题4．(江苏省无锡市部分学校2010年4月联考试卷)(16分)已知函数。

(1)若证明：对于任意的两个正数，总有成立；

(2)若对任意的，不等式：恒成立，求的取值范围。

　　　　 即：

题5．(连云港市2010届高三二模试题)(16分)设m为实数，函数， .

(1)若≥4，求m的取值范围；

(2)当m＞0时，求证在上是单调递增函数；

(3)若对于一切，不等式≥1恒成立，求实数m的取值范围

②　 当时，　　 　　　　　　　　

易证 　在为递增，由②得在为递增，

所以，，即，　 所以 。　　　　　 (14分)　　　　　　

③当时， 　(无解)　　　　　　　 (15分)　　　

综上所述　 。　　　　　　　　　　　　　　　　　　　 (16分)　

题6．(苏南六校2010年高三年级联合调研考试)(本小题满分16分)

已知函数 ，

(Ⅰ)若在上存在最大值与最小值，且其最大值与最小值的和为，试求和的值。

(Ⅱ)若为奇函数，

(1)是否存在实数，使得在为增函数，为减函数，若存在，求出的值，若不存在，请说明理由；

(2)如果当时，都有恒成立，试求的取值范围。

23．以下是美国某总统在1971年的一次演说：“西欧和日本…在经济的领导问题上……在全世界同我们竞争得非常激烈。……同我们在第二次世界大战结束的时候相比，美国遇到了我们甚至连做梦都没有想到过的那种挑战。”该总统是

　　 A．罗斯福　　 　 B．杜鲁门　　 　　　 C．艾森豪威尔　　 　 D．尼克松

22．在“三十年代大萧条”时期，主要的资本主义工业国都采取了一系列增加就业的措施。其中美国实行的主要措施是

　　 A．兴办公共工程　 B．发展军事工业　 C．调整农业生产　　 D．加强殖民掠夺

21．法国资产阶级在对封建制度的改造中，基本上实现了资产阶级争取经济自由、政治平等的革命目标的标志是

A．制宪会议颁布的八月法令与《人权宣言》　　

B．国民公会处死路易十六，建立共和国

C．雅各宾派废除封建权利，解决农民的土地问题　　

D．拿坡仑制定《民法典》和其他几部法典

20．以下属于开辟新航路所带来的后果的有　 ①西、葡两国扩大了资本　 ②意大利的商业地位削弱　 ③扩大了欧洲与亚洲、非洲之间的贸易　　 ④加速了西欧封建制度的衰落　

A．①②③　　 　 B．②③④　　 　　　 C．①③④　 　　　　 D．①②④

19．新航路开辟的根本原因是

　　 A．欧洲商品经济的发展　　　　 　　　 B．天文地理知识的进步

　　 C．《马可·波罗行纪》的流传　　 　　　 D．西、葡专制王室的支持

18．16世纪晚期，山东某地开始出现“地多烟草、木棉，专卖四方，五谷之利不及其半”的情况。这说明当时该地

　　 ①农业经济衰退　 ②农业结构发生变化　 ③商品经济发展　 ④农产品加工兴盛

A．①②　 　 　　 B．②③　　 　　　　 C．③④　 　　　　　 D．①③