
4.已知两点M(-2,0)、N(2,0),点P为坐标平面内的动点,满足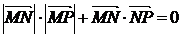 ,则动点P(x,y)的轨迹方程为( B )
,则动点P(x,y)的轨迹方程为( B )
(A)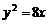 (B)
(B)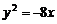 (C)
(C)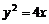 (D)
(D)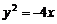
3.设过点P(x,y)的直线分别与x轴的正半轴和y轴的正半轴交于A,B两点,点Q与点P关于y轴对称,O为坐标原点,若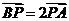 且
且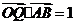 ,则点P的轨迹方程是( D )
,则点P的轨迹方程是( D )
A.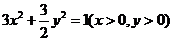 B.
B.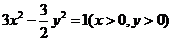
C.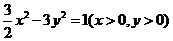 D.
D.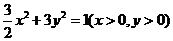
2.已知双曲线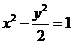 的焦点为F1、F2,点M在双曲线上且
的焦点为F1、F2,点M在双曲线上且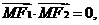 则点M到x轴的距离为(C)
则点M到x轴的距离为(C)
(A)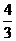 (B)
(B)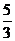 (C)
(C)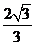 (D)
(D)
1.点P(-3,1)在椭圆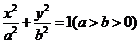 的左准线上.过点P且方向为a=(2,-5)的光线,经直线
的左准线上.过点P且方向为a=(2,-5)的光线,经直线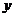 =-2反射后通过椭圆的左焦点,则这个椭圆的离心率为(A )
=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为(A )
( A ) 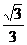 (
B )
(
B ) 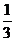 (
C )
(
C ) 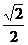 ( D )
( D )
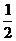
7.曲线x2+y2+x-6y+3=0上两点P、Q满足:①关于直线kx-y+4=0对称;②OP^OQ.求直线PQ的方程.
解:由圆上两点P、Q关于直线kx-y+4=0对称知直线kx-y+4=0经过圆心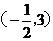
即有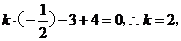
设直线PQ方程为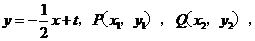
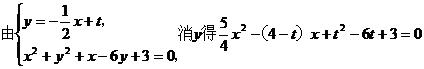 .
.
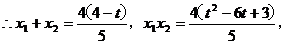
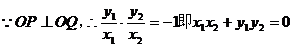 .
.
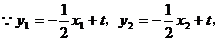
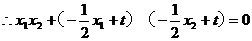
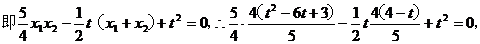
化简得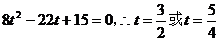
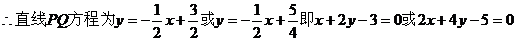 8. 已知△ABC的三边长分别为3、4、5,点P是它的内切圆上一点,求分别以PA、PB、PC为直径的三个圆面积之和的最大值和最小值。
8. 已知△ABC的三边长分别为3、4、5,点P是它的内切圆上一点,求分别以PA、PB、PC为直径的三个圆面积之和的最大值和最小值。
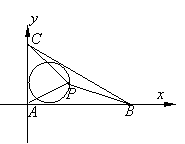 解:△ABC为直角三角形,如图建立直角坐标系,
解:△ABC为直角三角形,如图建立直角坐标系,
则A(0,0)、B(4,0)、C(0,3),设内切圆半
径为r,则r=1/2(|OC|+|OB|-|BC|)=1,故内切圆方程为
(x-1)2+(y-1)2=1,
可设P点坐标(1+cosα,1+sinα)
则以PA、PB、PC为直径的三个圆面积之和
S=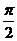 (10-cosα)
(10-cosα)
当cosα=-1时,Smax=5.5π,
当cosα=1时, Smin=4.5π.
6.关于曲线C:x2+y4=1的下列说法:(1)关于点(0,0)对称;(2)关于直线x轴对称;(3)关于直线y=x对称;(4)是封闭图形,面积小于p;(5)是封闭图形,面积大于p;(6)不是封闭图形,无面积可言.其中正确的序号是_________________.(1)(2)(4)
5.已知直线ax+by+c=0与圆O:x2+y2=1相交于A、B两点,且|AB|=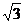 ,则
,则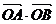 = .
= . 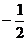
4.过点P(1,2)作一直线,使此直线与点M(2,3)和点N(4,-5)的距离相等,则此直线方程为___________________4x+y-6=0或3x+2y-7=0
3.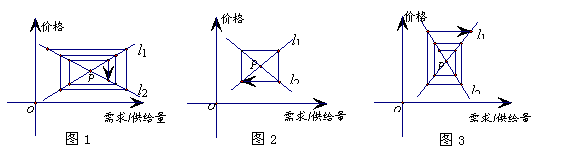 经济学中的“蛛网理论”(如图),假定某种商品的“需求-价格”函数的图象为直线l1,“供给-价格”函数的图象为直线l2,它们的斜率分别为k1、k2,l1与l2的交点P为“供给-需求”均衡点,在供求两种力量的相互作用下,该商品的价格和产销量,沿平行于坐标轴的“蛛网”路径,箭头所指方向发展变化,最终能否达于均衡点P,与直线l1、 l2的斜率满足的条件有关,从下列三个图中可知最终能达于均衡点P的条件为( A )
经济学中的“蛛网理论”(如图),假定某种商品的“需求-价格”函数的图象为直线l1,“供给-价格”函数的图象为直线l2,它们的斜率分别为k1、k2,l1与l2的交点P为“供给-需求”均衡点,在供求两种力量的相互作用下,该商品的价格和产销量,沿平行于坐标轴的“蛛网”路径,箭头所指方向发展变化,最终能否达于均衡点P,与直线l1、 l2的斜率满足的条件有关,从下列三个图中可知最终能达于均衡点P的条件为( A )
A.k1+k2>0 B.k1+k2=0 C.k1+k2<0 D.k1+k2可取任意实数
2.若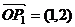 ,
,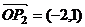 ,且
,且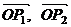 分别是直线l1:ax+(b-a)y-a=0,l2:ax+4by+b=0的方向向量,则a,b的值分别可以是(A)
分别是直线l1:ax+(b-a)y-a=0,l2:ax+4by+b=0的方向向量,则a,b的值分别可以是(A)
A.2,1 B.1,2 C.-1,2 D.-2,1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com