
重庆江津市高2007级四校联考
数学试卷(理科)
(五中、六中、几江、八中)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分.全卷共三个大题,22个小题,满分150分,考试时间为120分钟.
注意事项:
1.答卷前,考生务必将自己的学校、班级、姓名、考号填写在答题卡上.
2.第I卷每小题选出答案后,用笔填写在答题卡上“第I卷答题栏”对应题目的答案栏内.不能答在试题纸上.
3.第II卷各题一定要做在答题卡限定的区域内.
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)函数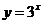 的反函数是
的反函数是
(A) 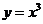 (B)
(B) 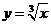 (C)
(C)  (D)
(D) 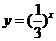
(2)将函数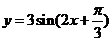 的图象按向量
的图象按向量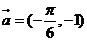 平移后所得图象的解析式是
平移后所得图象的解析式是
(A) 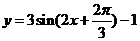 (B)
(B) 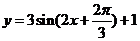
(C) 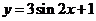 (D)
(D)

(3)在区间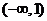 上递增的函数是
上递增的函数是
(A)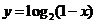 (B)
(B) 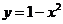 (C)
(C) 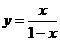 (D)
(D) 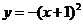
(4)函数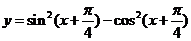 是
是
(A) 周期为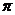 的奇函数 (B) 周期为
的奇函数 (B) 周期为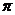 的偶函数
的偶函数
(C) 周期为2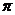 的奇函数 (D) 周期为2
的奇函数 (D) 周期为2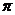 的偶函数
的偶函数
(5)已知集合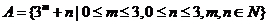 ,则集合A中元素个数为
,则集合A中元素个数为
(A) 16 (B)14 (C)9 (D)8
(6)条件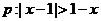 ,条件
,条件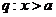 ,若p是q的充分不必要条件,则a的取值范围是
,若p是q的充分不必要条件,则a的取值范围是
(A) 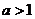 (B)
(B) 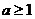 (C)
(C) 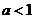 (D)
(D) 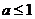
(7)定义在R上的函数 f (x) 在x ≥1时,f (x) = log 2 x ,且 f(x +1) 是偶函数。则f (0)=
(A) 0 (B) 1 (C) -1 (D) 2
(8))已知过点P(-2,2)且垂直于向量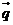 =(3,4)的直线与圆
=(3,4)的直线与圆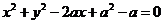 相切,则实数a的值为
相切,则实数a的值为
(A) 4 (B) 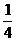 (C) 4或
(C) 4或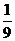 (D) -1或
(D) -1或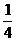
(9)已知曲线 上一点P到点A(-2,0)、点B(2,0)的距离之差为2,则△PAB是
上一点P到点A(-2,0)、点B(2,0)的距离之差为2,则△PAB是
(A)锐角三角形 (B) 直角三角形 (C)钝角三角形 (D) 等腰三角形
(10设数列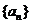 的前n项和为
的前n项和为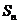 ,令
,令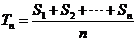 ,称
,称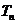 为数列
为数列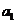 ,
,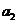 ,……,
,……,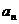 的“理想数”,已知数列
的“理想数”,已知数列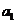 ,
,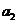 ,……,
,……,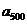 的“理想数”为2004,那么数列2,
的“理想数”为2004,那么数列2, 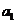 ,
,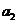 ,……,
,……,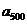 的“理想数”为
的“理想数”为
(A) 2002 (B) 2004 (C) 2006 (D) 2008
江津市2007级四校联考试题
数 学
第二部分 非选择题 (共100分)
(11 不等式4 x - 2 x +1 < 0 的解集是 。
二、填空题(本大题每小题4分,共24分。)
(12)已知向量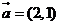 ,
,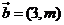 ,若
,若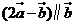 ,则m的值是 .
,则m的值是 .
(13)在条件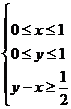 下,则
下,则 的最大值是
.
的最大值是
.
(14)设有两个命题:①关于x的不等式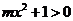 的解集是R,②函数
的解集是R,②函数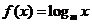 是减函数.如果这两个命题中有且只有一个真命题,则实数m的取值范围是
.
是减函数.如果这两个命题中有且只有一个真命题,则实数m的取值范围是
.
(15) 已知数列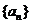 满足
满足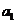 =24,且
=24,且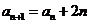 ,那么
,那么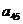 =
.
=
.
(16) .已知函数 f(x) =?x ? n ?0.5?,x∈[n, n+1 ),n是整数。 以下有四个命题
①f(x)是奇函数。 ②f(x)是偶函数。 ③f(x)是周期函数。④f(x) ≤0.5
其中正确命题的序号是____________。
(17)(本小题满分13分)
三、解答题:(本大题共6小题,共76分)
已知向量 ,
, .
.
(Ⅰ)当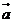 ⊥
⊥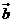 时,求|
时,求|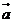 +
+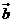 |的值;
|的值;
(Ⅱ)求函数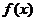 =
=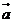 ?(
?(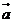 -
-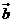 )的值域.
)的值域.
(18)(本小题满分13分)
已知函数 ,当
,当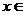 (
(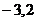 )时,
)时,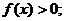 当
当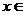 (
(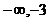 )
)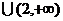 时,
时,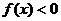
(Ⅰ)求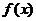 在[0,1]内的值域;
在[0,1]内的值域;
(Ⅱ)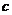 为何值时,
为何值时,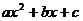 ≤0的解集为R.
≤0的解集为R.
(19)(本小题满分13分)
设数列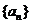 的前n项和为
的前n项和为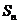 ,数列
,数列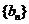 的前n项和为
的前n项和为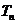 ,已知
,已知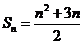 ,
,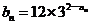 .
.
(Ⅰ)求数列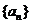 的通项公式;
的通项公式;
(Ⅱ)是否存在一个最小正整数M,当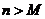 时,
时,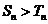 恒成立?若存在,求出这个M的值;若不存在,请说明理由.
恒成立?若存在,求出这个M的值;若不存在,请说明理由.
(20)(本小题满分13分)
已知函数f(x)= ax +
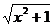 是R上的减函数,求a 的范围。
是R上的减函数,求a 的范围。
(21)(本小题满分12分)
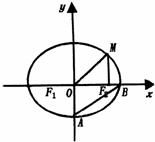
如图,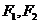 分别是椭圆
分别是椭圆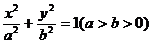 的左右焦点,M为椭圆上一点,
的左右焦点,M为椭圆上一点,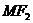 垂直于
垂直于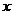 轴,且OM与椭圆长轴和短轴端点的连线AB平行,
轴,且OM与椭圆长轴和短轴端点的连线AB平行,
(Ⅰ)求椭圆的离心率;
(Ⅱ)若G为椭圆上不同于长轴端点任一点,求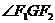 取值范围;
取值范围;
(Ⅲ)过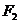 且与OM垂直的直线交椭圆于P,Q.若
且与OM垂直的直线交椭圆于P,Q.若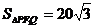 ,求椭圆的方程.
,求椭圆的方程.
(22)(本小题满分12分)
已知函数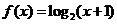 ,当点M(x,y)在
,当点M(x,y)在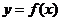 的图象上运动时,点N
的图象上运动时,点N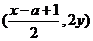 (
(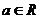 )在函数
)在函数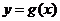 的图象上运动.
的图象上运动.
(Ⅰ)求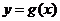 的解析式;
的解析式;
(Ⅱ)若函数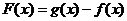 的最小值为4,求函数
的最小值为4,求函数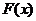 的单调区间;
的单调区间;
二、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
C
A
B
C
B
C
A
三、填空题
(11){x│x<1 } (12)  (13) 3 (14)m=0或m≥1 (15) 2004
(13) 3 (14)m=0或m≥1 (15) 2004
(16)②③④
三解答题
(17)(Ⅰ) ; (Ⅱ)
; (Ⅱ) .
.
(18)解:由题目知 的图像是开口向下,交
的图像是开口向下,交 轴于两点
轴于两点 和
和 的抛物线,对称轴方程为
的抛物线,对称轴方程为 (如图)
(如图)
那么,当 和
和 时,有
时,有 ,代入原式得:
,代入原式得:

解得: 或
或 
经检验知: 不符合题意,舍去.
不符合题意,舍去.

(Ⅰ)由图像知,函数在 内为单调递减,所以:当
内为单调递减,所以:当 时,
时, ,当
,当 时,
时, .
.
 在
在 内的值域为
内的值域为
(Ⅱ)令
要使 的解集为R,则需要方程
的解集为R,则需要方程 的根的判别式
的根的判别式 ,即
,即
解得 
 当
当 时,
时, 的解集为R.
的解集为R.
(19)(Ⅰ) ; (Ⅱ)存在M=4.
; (Ⅱ)存在M=4.
(20)解:任设x 1>x2
f(x 1)-f(x2) = a x 1+ - a x 2 -
- a x 2 -
=(x 1-x 2)(a+  )
)
∵f(x)是R上的减函数,
∴(x 1-x
2)(a+  )<0恒成立
)<0恒成立
又 <1
<1
∴a≤ -1
(21)解:(Ⅰ)由已知


 ,
,
(Ⅱ)设 ,
,

当且仅当 时,
时,

(Ⅲ)




 椭圆的方程为
椭圆的方程为
(22)(Ⅰ) .
.
(Ⅱ) 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com